
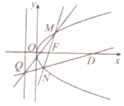
 已知抛物线ω:y2=ax(a>0)上一点,P(t,2)到焦点F的距离为2t
已知抛物线ω:y2=ax(a>0)上一点,P(t,2)到焦点F的距离为2t分析 (Ⅰ)根据抛物线的定义,可得a=4t,将P代入抛物线方程,求得at=4,代入即可求得a的值,求得抛物线ω的方程;
(Ⅱ)设A(x1,y1),B(x2,y2),设直线MN的方程为x=my+1,联立方程组,表示出直线ND的方程,与抛物线ω的准线方程构成方程组,解得Q的坐标,求出直线MQ的斜率,得到直线MQ的方程,求出交点坐标即可.
解答 解:(Ⅰ)由抛物线的定义可知丨PF丨=t+$\frac{a}{4}$=2t,则a=4t,
由点P(t,2)在抛物线上,则at=4,
∴a×$\frac{a}{4}$=4,则a2=16,
由a>0,则a=4,
∴抛物线的方程y2=4x;
(Ⅱ)证明:设M(x1,y1),N(x2,y2),
设直线MN的方程为x=my+1
$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+1}\end{array}\right.$,整理得:y2-4my-4=0,
由韦达定理可知:y1•y2=-4,
依题意,直线ND与x轴不垂直,∴x2=4.
∴直线ND的方程可表示为,y=$\frac{{y}_{2}}{{x}_{2}-4}$(x-4)①
∵抛物线ω的准线方程为,x=-1②
由①,②联立方程组可求得Q的坐标为(-1,-$\frac{5{y}_{2}}{{x}_{2}-4}$)
∴Q的坐标可化为(-1,$\frac{5{y}_{1}}{1-{y}_{1}^{2}}$),
∴kMQ=$\frac{\frac{5{y}_{1}}{1-{y}_{1}^{2}}-{y}_{1}}{-1-{x}_{1}}$,
∴直线MQ的方程为y-y1=$\frac{4{y}_{1}}{{y}_{1}^{2}-1}$(x-x1),
令y=0,可得x=x1-$\frac{{y}_{1}^{2}-1}{4}$=$\frac{1}{4}$,
∴直线MQ与x轴交于定点($\frac{1}{4}$,0).
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查直线过定点,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 合情推理法 | B. | 综合法 | C. | 间接证法 | D. | 分析法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{14}{13}$,+∞) | B. | [$\frac{13}{12}$,+∞) | C. | [$\frac{15}{13}$,2) | D. | [$\frac{5}{4}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
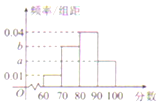 某校高三年级的一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取100人了解情况,已知70~80分数段抽取了30人,则全体高三年级学生的平均分数为82(以各组区间的中点值代表改组的取值)
某校高三年级的一次测验成绩的频率分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取100人了解情况,已知70~80分数段抽取了30人,则全体高三年级学生的平均分数为82(以各组区间的中点值代表改组的取值)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
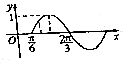 函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1,x2∈($\frac{π}{6}$,$\frac{2π}{3}$)且x1,x2是方程f(x)=m的两个实数根,其中m∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则f(x1+x2)=( )| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ | $\frac{7π}{3}$ | $\frac{17π}{6}$ |
| f(x) | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com