
| A. | ($\sqrt{10}$,0) | B. | (0,10) | C. | (10,+∞) | D. | (1,10) |
分析 转化已知条件,通过构造函数,利用函数的单调性,求解不等式的解集即可.
解答 解:定义在(0,+∞)上的函数f(x)满足x2f'(x)+1>0,
可得:f'(x)+$\frac{1}{{x}^{2}}$>0,构造函数g(x)=f(x)-$\frac{1}{x}$-5,则g′(x)=f′(x)$+\frac{1}{{x}^{2}}$>0,所以g(x)在(0,+∞)上是增函数,
∵f(1)=6,∴g(1)=0,故g(x)<0的解集为:(0,1).即f(x)<$\frac{1}{x}$+5的解集为(0,1),由0<lgx<1,
可得1<x<10.
所求不等式的解集为:(1,10).
故选:D.
点评 本题考查函数的导数的应用,函数的单调性与导数的关系,解题的难点是构造函数,转化思想的应用.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:选择题
| A. | 既有最大值,又有最小值 | B. | 只有最小值,没有最大值 | ||
| C. | 只有最大值,没有最小值 | D. | 既无最大值,也无最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x∈[0,\frac{π}{2})$ | B. | $(\frac{π}{2},π]$ | C. | $[π,\frac{3π}{2})$ | D. | $(\frac{3π}{2},2π]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
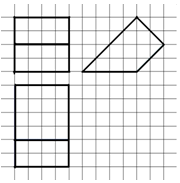 如图,网格上小正方形的边长为$\frac{1}{2}$,粗线画出的是某空间几何体的三视图,则该几何体的体积为( )
如图,网格上小正方形的边长为$\frac{1}{2}$,粗线画出的是某空间几何体的三视图,则该几何体的体积为( )| A. | 24 | B. | 12 | C. | 4 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com