
分析 (1)根据直线的斜率k=$\frac{cosα}{sinα}$,α=$\frac{π}{3}$时,可求出直线l的斜率;
(2)利用参数的几何意义求解,设A,B两点对应的参数分别为tA,tB,把直线l的方程代入圆O的方程中,在根据且|PA|,|OP|,|PB|成等比数列,可得动点P的轨迹方程.
解答 解:(1)当α=$\frac{π}{3}$时,直线l的斜率k=$\frac{cosα}{sinα}$=$\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{3}$;
(2)由题意,设A,B两点对应的参数分别为tA,tB,
把直线l的方程代入圆O的方程中,(a+tsinα)2+(b+tcosα)2=4
整理得:t2+(2asinα+2bcosα)t+a2+b2-4=0.
∴tA•tB=a2+b2-4=-|PA|•|PB|
又∵|PA|,|OP|,|PB|成等比数列,
∴||OP|2=|PB|•|PA|
∴-(a2+b2-4)=a2+b2即a2+b2=2
∴动点P的轨迹方程为x2+y2=2.
点评 本题考查了直线参数方程的几何意义,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | 3f (ln2)<2 f (ln3) | B. | 3 f (ln2)=2 f (ln3) | ||
| C. | 3 f(ln2)>2 f (ln3) | D. | 3 f (ln2)与2 f (ln3)的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 八卦 |  |  | 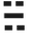 | 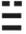 | … |  | … |
| 二进制 | 000 | 001 | 010 | 011 | … | A | … |
| 十进制 | 0 | 1 | 2 | 3 | … | B | … |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
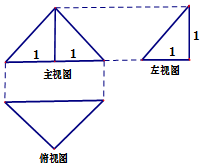
| A. | $\frac{4}{3}π$ | B. | $\frac{{\sqrt{3}}}{2}π$ | C. | $\frac{{5\sqrt{5}}}{6}π$ | D. | $\sqrt{6}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
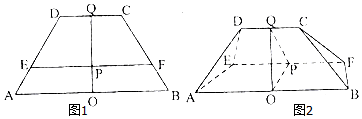
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com