
| A. | m≤1或m≥2 | B. | 2≤m≤8 | C. | -2≤m≤10 | D. | m≤-2或m≥8 |
分析 若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心(-1,2)到直线l的距离$d=\frac{|-m-2+2m-2+4-4m|}{{\sqrt{{{(m+2)}^2}+{{(m-1)}^2}}}}≤2$,即可求出实数m的取值范围.
解答 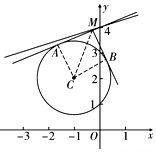 解:如图,设切点分别为A,B.连接AC,BC,MC,
解:如图,设切点分别为A,B.连接AC,BC,MC,
由∠AMB=∠MAC=∠MBC=90°及MA=MB知,四边形MACB为正方形,故$|MC|=\sqrt{2+2}=2$,
若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心(-1,2)到直线l的距离$d=\frac{|-m-2+2m-2+4-4m|}{{\sqrt{{{(m+2)}^2}+{{(m-1)}^2}}}}≤2$,即m2-8m-20≤0,∴-2≤m≤10,
故选:C.
点评 本题考查直线和圆的位置关系,由题意得到若直线l上总存在点M使得过点M的两条切线互相垂直,只需圆心(-1,2)到直线l的距离$d=\frac{|-m-2+2m-2+4-4m|}{{\sqrt{{{(m+2)}^2}+{{(m-1)}^2}}}}≤2$,是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 26 | C. | 20 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | T有最大值2 | B. | T有最小值1 | ||
| C. | T有最大值1 | D. | T没有最大值和最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{{({{a^x}+1})x}}{{{a^x}-1}}({a>0,a≠1})$ | B. | $y=\frac{{{a^x}-{a^{-x}}}}{2}({a>0,a≠1})$ | ||
| C. | $y=\left\{\begin{array}{l}1,({x>0})\\-1,({x<0})\end{array}\right.$ | D. | $y={log_a}\frac{1+x}{1-x}({a>0,a≠1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com