
分析 (Ⅰ)老远函数的奇偶性的定义先判定函数的奇偶性.所有的基本事件包括两类:一类为两张卡片上写的函数均为奇函数;另一类为两张卡片上写的函数为一个是奇函数,一个为偶函数;可得基本事件总数.再利用古典概率计算公式即可得出.
(II)老远古典概率计算公式、相互独立事件的概率计算公式可得概率,分布列及其数学期望.
解答 解:(Ⅰ)f1(x)=x3为奇函数,f2(x)=5|x|,为偶函数,f3(x)=2为偶函数,f4(x)=$\frac{1}{x}$为奇函数,f5(x)=sin($\frac{π}{2}$-x)=cosx为偶函数,f6(x)=xcosx为奇函数.
所有的基本事件包括两类:一类为两张卡片上写的函数均为奇函数;
另一类为两张卡片上写的函数为一个是奇函数,一个为偶函数;故基本事件总数为${∁}_{3}^{1}{∁}_{3}^{1}$+${∁}_{3}^{2}$=12.
满足条件的基本事件为两张卡片上写的函数均为奇函数,故满足条件的基本事件个数为${∁}_{3}^{2}$.
故所求概率为P=$\frac{{∁}_{3}^{2}}{12}$=$\frac{1}{4}$.
(Ⅱ)ξ可取1,2,3,4. P(ξ=1)=$\frac{{∁}_{3}^{1}}{{∁}_{6}^{1}}$=$\frac{1}{2}$,P(ξ=2)=$\frac{{∁}_{3}^{1}}{{∁}_{6}^{1}}$•$\frac{{∁}_{3}^{1}}{{∁}_{5}^{1}}$=$\frac{3}{10}$,
P(ξ=3)=$\frac{{∁}_{3}^{1}}{{∁}_{6}^{1}}$•$\frac{{∁}_{2}^{1}}{{∁}_{5}^{1}}$•$\frac{{∁}_{3}^{1}}{{∁}_{4}^{1}}$=$\frac{3}{20}$,P(ξ=4)=$\frac{{∁}_{3}^{1}}{{∁}_{6}^{1}}$•$\frac{{∁}_{2}^{1}}{{∁}_{5}^{1}}$•$\frac{{∁}_{1}^{1}}{{∁}_{4}^{1}}$•$\frac{{∁}_{3}^{1}}{{∁}_{3}^{1}}$=$\frac{1}{20}$.
故ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{1}{2}$ | $\frac{3}{10}$ | $\frac{3}{20}$ | $\frac{1}{20}$ |
点评 本题考查了相互独立事件的概率计算公式、随机变量的分布列及其数学期望计算公式、函数的奇偶性,考查了推理能力与计算能力,属于中档题.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤1或m≥2 | B. | 2≤m≤8 | C. | -2≤m≤10 | D. | m≤-2或m≥8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 选择套餐种类 | A | B | C |
| 选择每种套餐的人数 | 50 | 25 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 八卦 |  |  | 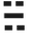 | 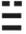 | … |  | … |
| 二进制 | 000 | 001 | 010 | 011 | … | A | … |
| 十进制 | 0 | 1 | 2 | 3 | … | B | … |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
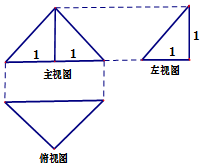
| A. | $\frac{4}{3}π$ | B. | $\frac{{\sqrt{3}}}{2}π$ | C. | $\frac{{5\sqrt{5}}}{6}π$ | D. | $\sqrt{6}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{5}{3}})$和(1,+∞) | B. | $({-∞,-\frac{5}{3}})∪$(1,+∞) | C. | (-∞,-1)和$({\frac{5}{3},+∞})$ | D. | (-∞,-1)∪$({\frac{5}{3},+∞})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com