
分析 (Ⅰ)利用抛物线的定义,即可求动点M的轨迹E的方程;
(Ⅱ)由题意可设直线l':x=my+n,由$\left\{{\begin{array}{l}{x=my+n}\\{{y^2}=4x}\end{array}}\right.$可得y2-4my-4n=0,求出A,P的坐标,利用向量的数量积,即可得出结论.
解答 解:(Ⅰ)设动点M(x,y),
由抛物线定义可知点M的轨迹E是以N(1,0)为焦点,直线l:x=-1为准线的抛物线,
所以轨迹E的方程为y2=4x.
(Ⅱ)点N在以PA为直径的圆C上.
理由:由题意可设直线l':x=my+n,
由$\left\{{\begin{array}{l}{x=my+n}\\{{y^2}=4x}\end{array}}\right.$可得y2-4my-4n=0(*),
因为直线l'与曲线E有唯一公共点A,
所以△=16m2+16n=0,即n=-m2.
所以(*)可化简为y2-4my+4m2=0,
所以A(m2,2m),
令x=-1得$P(-1,-\frac{1+n}{m})$,
因为n=-m2,
所以$\overrightarrow{NA}•\overrightarrow{NP}=({m^2}-1,2m)•(-2,-\frac{1+n}{m})=-2{m^2}+2-2-2n=0$
所以NA⊥NP,
所以点N在以PA为直径的圆C上.
点评 本题考查抛物线的定义与方程,考查直线与抛物线位置关系的运用,考查向量知识,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{10}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{4\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
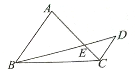 如图所示,AC与BD交于点E,AB∥CD,AC=3$\sqrt{5}$,AB=2CD=6,当tanA=2时,$\overrightarrow{BE}•\overrightarrow{DC}$=-12.
如图所示,AC与BD交于点E,AB∥CD,AC=3$\sqrt{5}$,AB=2CD=6,当tanA=2时,$\overrightarrow{BE}•\overrightarrow{DC}$=-12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $-\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com