
分析 (Ⅰ)先求导,再根据题意可得f′(1)=e,f(1)=0,解得即可,
(Ⅱ)结合(Ⅰ)根据定积分的计算法则计算即可.
解答 解:(Ⅰ)因为f(x)=(kx+b)•ex,
所以f′(x)=(kx+k+b)ex,
依题意:f′(1)=e,f(1)=0,
即$\left\{\begin{array}{l}{(2k+b)e=e}\\{(k+b)e=0}\end{array}\right.$解得k=1,b=-1.
(Ⅱ)由(Ⅰ)知f(x)=(x-1)•ex,
f'(x)=x•ex,
所以$\int_0^1{(x•{e^x})dx=\left.{(x-1)•{e^x}}\right|\begin{array}{l}1\\ 0\end{array}}$=0+1=1.
点评 本题主要考查导数的几何意义和定积分的计算,属于基础题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧q | C. | p∧?q | D. | ?p∧?q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①② | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | r越大,两变量的线性相关性越强 | B. | R2越大,两变量的线性相关性越强 | ||
| C. | r的取值范围为(-∞,+∞) | D. | R2的取值范围为[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 | |
| 使用淡化海砂 | 25 | t | 30 |
| 使用未经淡化海砂 | s | ||
| 总计 | 40 | 60 |
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
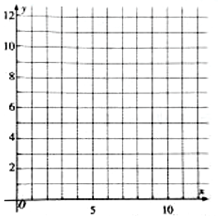 为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如图所示(x(吨)为买进蔬菜的质量,y(天)为销售天数):
为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如图所示(x(吨)为买进蔬菜的质量,y(天)为销售天数):| x | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| y | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com