Question

10£®ÎªÁ˸üºÃµØ¹æ»®½ø»õµÄÊýÁ¿£¬±£Ö¤Ê߲˵ÄÐÂÏʳ̶ȣ¬Ä³Êß²ËÉ̵ê´ÓijһÄêµÄÏúÊÛÊý¾ÝÖУ¬Ëæ»ú³éÈ¡ÁË8×éÊý¾Ý×÷ΪÑо¿¶ÔÏó£¬ÈçͼËùʾ£¨x£¨¶Ö£©ÎªÂò½øÊ߲˵ÄÖÊÁ¿£¬y£¨Ì죩ΪÏúÊÛÌìÊý£©£º

x	2	3	4	5	6	7	9	12
y	1	2	3	3	4	5	6	8

£¨¢ñ£©¸ù¾ÝÉϱíÊý¾ÝÔÚÏÂÁÐÍø¸ñÖлæÖÆÉ¢µãͼ£»
£¨¢ò£©¸ù¾ÝÉϱíÌṩµÄÊý¾Ý£¬ÓÃ×îС¶þ³Ë·¨Çó³öy¹ØÓÚxµÄÏßÐԻع鷽³Ì$\hat y=\hat bx+\hat a$£»
£¨¢ó£©¸ù¾Ý£¨¢ò£©ÖеļÆËã½á¹û£¬Èô¸ÃÊß²ËÉ̵ê×¼±¸Ò»´ÎÐÔÂò½ø25¶Ö£¬ÔòÔ¤¼ÆÐèÒªÏúÊÛ¶àÉÙÌ죮
²Î¿¼¹«Ê½£º$\hat b=\frac{{\sum_{i=1}^n{£¨{{x_i}-\overline x}£©}£¨{{y_i}-\overline y}£©}}{{\sum_{i=1}^n{{{£¨{{x_i}-\overline x}£©}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$£¬$\hat a=\overline y-\hat b\overline x$£®

Answer 1

·ÖÎö £¨¢ñ£©¸ù¾ÝËù¸øÊý¾Ý»­³öÉ¢µãͼ¼´¿É£»
£¨¢ò£©Çó³öÖÐÐĵãµÄ×ø±ê£¬Çó³ö»¯¹é·½³ÌÖеÄϵÊý£¬´úÈë·½³Ì¼´¿É£»
£¨¢ó£©½«xµÄÖµ´úÈë·½³ÌÇó³ö¶ÔÓ¦µÄyµÄÖµ¼´¿É£®

½â´ð ½â£º£¨¢ñ£©É¢µãͼÈçͼËùʾ£º

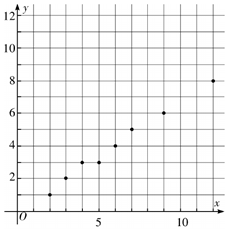
£¨¢ò£©ÒÀÌâÒ⣬$\overline x=\frac{1}{8}£¨{2+3+4+5+}\right.$6+7+9+12£©=6£¬$\overline y=\frac{1}{8}£¨{1+2+3+4}\right.$+5+6+8£©=4£¬
$\sum_{i=1}^8{x_i^2}=4+9+16+25$+36+49+81+144=364£¬$\sum_{i=1}^8{{x_i}{y_i}}=2+6+12+15+24$+35+54+96=244£¬
$\hat b=\frac{{\sum_{i=1}^8{{x_i}{y_i}-8\overline x\overline y}}}{{\sum_{i=1}^8{x_i^2}}}$=$\frac{244-8¡Á6¡Á4}{{364-8¡Á{6^2}}}=\frac{13}{19}$£¬¡à$\hat a=4-\frac{13}{19}¡Á6=-\frac{2}{19}$£¬
¡à»Ø¹éÖ±Ïß·½³ÌΪ$\hat y=\frac{13}{19}x-\frac{2}{19}$£®
£¨¢ó£©ÓÉ£¨¢ò£©Öª£¬µ±x=25ʱ£¬$y=\frac{13}{19}¡Á25-$$\frac{2}{19}=17$£®
¼´ÈôÒ»´ÎÐÔÂò½øÊß²Ë25¶Ö£¬ÔòÔ¤¼ÆÐèÒªÏúÊÛ17Ì죮

µãÆÀ ±¾Ì⿼²éÁËÉ¢µãͼÎÊÌ⣬¿¼²éÇó»Ø¹é·½³ÌÎÊÌ⣬ÊÇÒ»µÀÖеµÌ⣮