
分析 由定积分的几何意义知:${∫}_{0}^{1}$$\sqrt{4-{x}^{2}}$dx是如图所示的阴影部分曲边梯形OABC的面积,其面积可分为扇形和三角形,分别求解即可,再根据定积分的计算法则
解答 解:${∫}_{-1}^{1}$$\sqrt{4-{x}^{2}}$dx=2${∫}_{0}^{1}$$\sqrt{4-{x}^{2}}$dx,
由定积分的几何意义知:${∫}_{0}^{1}$$\sqrt{4-{x}^{2}}$dx是如图所示的阴影部分曲边梯形OABC的面积,
其中B(1,$\sqrt{3}$),∠BOC=30°
故${∫}_{0}^{1}$$\sqrt{4-{x}^{2}}$dx=S扇形BOC+S△AOB=$\frac{π}{3}$+$\frac{\sqrt{3}}{2}$,
故${∫}_{-1}^{1}$$\sqrt{4-{x}^{2}}$dx=2${∫}_{0}^{1}$$\sqrt{4-{x}^{2}}$dx=$\frac{2π}{3}$+$\sqrt{3}$,
故${∫}_{-1}^{1}$e|x|dx=2${∫}_{0}^{1}$exdx=2ex|${\;}_{0}^{1}$=2e-2,
故$\int_{-1}^1{({{e^{|x|}}+\sqrt{4-{x^2}}})}dx$=$2e+\frac{2}{3}π-2+\sqrt{3}$,
故答案为:$2e+\frac{2}{3}π-2+\sqrt{3}$,
点评 本题考查定积分的几何意义,准确转化为图形的面积是解决问题的关键,属于中档题


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧q | C. | p∧?q | D. | ?p∧?q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{15}{8}$ | D. | $\frac{17}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 260 | B. | 280 | C. | 300 | D. | 320 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①② | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
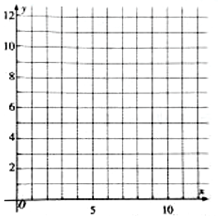 为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如图所示(x(吨)为买进蔬菜的质量,y(天)为销售天数):
为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如图所示(x(吨)为买进蔬菜的质量,y(天)为销售天数):| x | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| y | 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com