
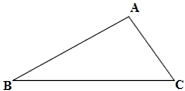
 如图,在△ABC中,BC、CA、AB的长分别为a,b,c,
如图,在△ABC中,BC、CA、AB的长分别为a,b,c,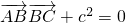 ,试证明△ABC为直角三角形.
,试证明△ABC为直角三角形.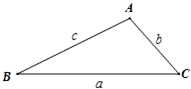 解:(1)∵
解:(1)∵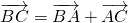 ,
,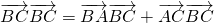
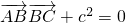 得
得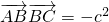 ,
,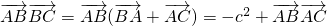
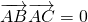 ,∴△ABC为直角三角形
,∴△ABC为直角三角形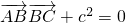 得,accos(π-B)+c2=0.即:c2=accosB
得,accos(π-B)+c2=0.即:c2=accosB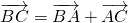 ,两边平方化简,即可证明a=bcosC+ccosB;
,两边平方化简,即可证明a=bcosC+ccosB;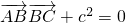 ,转化为
,转化为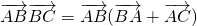 ,推出
,推出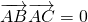 ,即可证明△ABC为直角三角形.
,即可证明△ABC为直角三角形.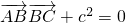 推出bcosA=0,说明A=90°即可.
推出bcosA=0,说明A=90°即可. 同向的单位向量
同向的单位向量 ,在
,在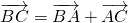 的两边作数量积,同样可证.
的两边作数量积,同样可证. 

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在△ABC中,设
如图,在△ABC中,设| AB |
| AC |
| AP |
| S平行四边形ANPM |
| S△ABC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com