
 如图,在△ABC中,AB=AC=1,∠BAC=120°.
如图,在△ABC中,AB=AC=1,∠BAC=120°.分析 (I)建立坐标系,求出向量坐标,代入数量积公式计算.
(II)根据模长列出方程,利用基本不等式解出最大值.
解答 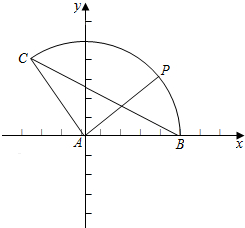 解:(1)以AB为x轴,以A为原点,建立坐标系,如图:
解:(1)以AB为x轴,以A为原点,建立坐标系,如图:
则A(0,0),B(1,0),C(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).$\overrightarrow{AB}$=(1,0),$\overrightarrow{BC}$=(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).∴$\overrightarrow{AB}$•$\overrightarrow{BC}$=-$\frac{3}{2}$.
(2)$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$=(x-$\frac{y}{2}$,$\frac{\sqrt{3}y}{2}$).
∵|$\overrightarrow{AP}$|=1.∴(x-$\frac{y}{2}$)2+($\frac{\sqrt{3}y}{2}$)2=1.
∴x2+y2=1+xy≥2xy.∴xy≤1.
∴xy的最大值是1.
点评 本题考查了平面向量的数量积运算,基本不等式,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{CD}$ | B. | $\overrightarrow{DC}$ | C. | $\overrightarrow{AD}$ | D. | $\overrightarrow{CB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
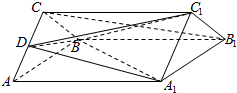 如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D
如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$,+∞) | B. | (1,$\sqrt{3}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com