
【题目】![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程.
处的切线方程.
(2)若函数![]() 在定义域上为单调增函数.
在定义域上为单调增函数.
①求![]() 的最大整数值;
的最大整数值;
②证明:![]() .
.
【答案】(1)![]() ;(2)① 2; ②证明见解析.
;(2)① 2; ②证明见解析.
【解析】
(1)求得![]() 时函数的解析式,求得
时函数的解析式,求得![]() 的值,结合直线的点斜式,即可求解;
的值,结合直线的点斜式,即可求解;
(2)由题意可得![]() 恒成立.
恒成立.
①先证明![]() ,设
,设![]() ,求得导数和单调性即可作出证明;同理可证得
,求得导数和单调性即可作出证明;同理可证得![]() ,再讨论
,再讨论![]() 和
和![]() ,即可求得
,即可求得![]() 的最大值.
的最大值.
②由①知![]() ,令
,令![]() ,可得
,可得![]() ,得到
,得到![]() ,利用累加结合等比数列的求和公式,即可求解.
,利用累加结合等比数列的求和公式,即可求解.
(1)当![]() 时,
时,![]() ,可得
,可得![]() ,
,
又由![]() ,则
,则![]() ,
,
则所求切线方程为![]() ,即
,即![]() .
.
(2)由函数![]() ,可得
,可得![]() ,
,
若函数![]() 在定义域上为单调增函数,则
在定义域上为单调增函数,则![]() 恒成立.
恒成立.
①先证明![]() ,设
,设![]() ,则
,则![]() ,
,
则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.
同理可证![]() ,
,
所以![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() 恒成立;
恒成立;
当![]() 时,
时,![]() ,不恒成立,
,不恒成立,
经检验![]() 符合题意.
符合题意.
综上所述,![]() 的最大整数值为2.
的最大整数值为2.
②证明:由①知![]() ,令
,令![]() ,
,
∴![]() ,∴
,∴![]() ,
,
由此可知,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
…,
当![]() 时,
时,![]() ,
,
累加得![]() .
.
又 ,
,
∴![]() ,
,
即![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() ,过点D作抛物线
,过点D作抛物线![]() 的切线l,切点A在第二象限.
的切线l,切点A在第二象限.
(1)求切点A的纵坐标.
(2)有一离心率为![]() 的椭圆
的椭圆![]() 恰好经过切点A,设切线l与椭圆
恰好经过切点A,设切线l与椭圆![]() 的另一交点为点B,切线l,
的另一交点为点B,切线l,![]() 的斜率分别为
的斜率分别为![]() ,若
,若![]() 成等差数列,求椭圆
成等差数列,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形。
都为矩形。

(Ⅰ)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论。
?请证明你的结论。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向上平移2个单位长度,得到函数
个单位长度,再向上平移2个单位长度,得到函数![]() 的图象,则函数
的图象,则函数![]() 的图象与函数
的图象与函数![]() 的图象( )
的图象( )
A.关于直线![]() 对称B.关于直线
对称B.关于直线![]() 对称
对称
C.关于点![]() 对称D.关于点
对称D.关于点![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是我国南北朝时期杰出的数学家和天文学家祖冲之的儿子,他提出了一条原理:“幂势既同幂,则积不容异”.这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.一般大型热电厂的冷却塔大都采用双曲线型.设某双曲线型冷却塔是曲线![]()
![]() 与直线
与直线![]() ,
, ![]() 和
和![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周所得,如图所示.试应用祖暅原理类比求球体体积公式的方法,求出此冷却塔的体积为_______.
轴旋转一周所得,如图所示.试应用祖暅原理类比求球体体积公式的方法,求出此冷却塔的体积为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程。
已知曲线C![]() :
:![]() (t为参数), C
(t为参数), C![]() :
:![]() (
(![]() 为参数)。
为参数)。
(1)化C![]() ,C
,C![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C![]() 上的点P对应的参数为
上的点P对应的参数为![]() ,Q为C
,Q为C![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线
![]() (t为参数)距离的最小值。
(t为参数)距离的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABCD的底面为正方形,PD底面ABCD.设平面PAD与平面PBC的交线为![]() .
.
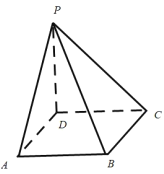
(1)证明:![]() 平面PDC;
平面PDC;
(2)已知PDAD1,Q为![]() 上的点,QB=
上的点,QB=![]() ,求PB与平面QCD所成角的正弦值.
,求PB与平面QCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式.某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取1名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com