
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)若经过原点![]() 的直线与椭圆
的直线与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,试判断
,试判断![]() 是否为定值?若为定值,试求出该定值;否则,请说明理由.
是否为定值?若为定值,试求出该定值;否则,请说明理由.
【答案】(1) 椭圆![]() 的方程为
的方程为![]() (2)见解析.
(2)见解析.
【解析】试题分析:(1)由题意知, ![]() 的周长,求得
的周长,求得![]() 的值,进而得到
的值,进而得到![]() 的值,从而求得椭圆的方程;
的值,从而求得椭圆的方程;
(2)①当直线![]() 在斜率不存在时,把
在斜率不存在时,把![]() 代入椭圆方程,即可求解
代入椭圆方程,即可求解![]() 的值;
的值;
②当直线![]() 的斜率
的斜率![]() 存在时,设其方程为
存在时,设其方程为![]() ,联立方程组,求得
,联立方程组,求得![]() ,利用弦长公式,求解
,利用弦长公式,求解![]() ,再根据因为
,再根据因为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,联立方程组,进而求得则
,联立方程组,进而求得则![]() ,即可得到结论.
,即可得到结论.
试题解析:
(1)由题意知, ![]() 的周长为
的周长为![]() ,所以
,所以![]() ,
,
又椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,
,
所以![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() ;
;
(2)①当直线![]() 在斜率不存在时,其方程为
在斜率不存在时,其方程为![]() ,代入椭圆方程得
,代入椭圆方程得![]() ,
,
不妨设![]() ,则
,则![]() ,
,
因为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,代入椭圆方程得
,代入椭圆方程得![]() ,
,
不妨设![]() ,则
,则![]() ,
,
所以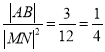 ;
;
②当直线![]() 的斜率
的斜率![]() 存在时,设其方程为
存在时,设其方程为![]() ,
,
由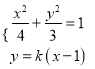 消去
消去![]() 得
得![]() ,
,
则![]() ,
,
![]() ,则
,则![]() ,
,
因为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,
由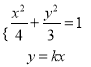 消去
消去![]() 得
得![]() ,则
,则![]() ,
,
则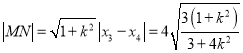 ,
,
所以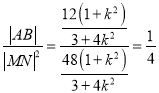 ,综上所述,
,综上所述, ![]() 为定值
为定值![]()


科目:高中数学 来源: 题型:
【题目】如图,已知平面![]()
![]() 平面
平面![]() ,
, ![]() 与
与![]() 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形, ![]() //
// ![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() //
// ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的重心,
的重心, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() //平面
//平面![]() ;
;
(Ⅱ)若直线![]() 与
与![]() 所成角为
所成角为![]() ,试求二面角
,试求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知![]() 且
且![]() 设
设![]() ,绿地面积为
,绿地面积为![]() .
.
(1)写出![]() 关于
关于![]() 的函数关系式,并指出这个函数的定义域.
的函数关系式,并指出这个函数的定义域.
(2)当![]() 为何值时,绿地面积
为何值时,绿地面积![]() 最大?
最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为A,B,C所对边,a+b=4,(2﹣cosA)tan ![]() =sinA.
=sinA.
(1)求边长c的值;
(2)若E为AB的中点,求线段EC的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】联合国教科文组织规定,每年的4月23日是“世界读书日”.某校研究生学习小组为了解本校学生的阅读情况,随机调查了本校400名学生在这一天的阅读时间![]() (单位:分钟),将时间数据分成5组:
(单位:分钟),将时间数据分成5组:![]() ,并整理得到如下频率分布直方图.
,并整理得到如下频率分布直方图.
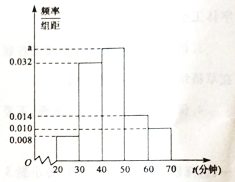
(1)求![]() 的值;
的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这400名学生中抽取50人参加交流会,则在阅读时间为![]() 的两组中分别抽取多少人?
的两组中分别抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是 . 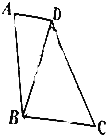
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点是坐标原点![]() ,焦点
,焦点![]() 在
在![]() 轴的正半轴上,过焦点
轴的正半轴上,过焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 两点,且满足
两点,且满足![]() .
.
(1)求抛物线的方程;
(2)已知![]() 为抛物线上一点,若点
为抛物线上一点,若点![]() 位于
位于![]() 轴下方且
轴下方且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:
组数 | 分组 | 认同人数 | 认同人数占 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |
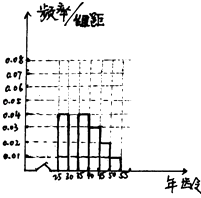
(1)完成所给频率分布直方图,并求n,a,p.
(2)若从[40,45),[45,50)两个年龄段中的“认同”人群中,按分层抽样的方法抽9人参与座谈会,然后从这9人中选2名作为组长,组长年龄在[40,45)内的人数记为ξ,求随机变量ξ的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com