
分析 由题意可得,g(x)=max{f(x1),f(x2)},作出函数g(x)的图象,$\frac{g({x}_{1})-g({x}_{2})}{{x}_{1}-{x}_{2}}$>0恒成立等价于函数为增函数,由图象得答案.
解答 解:由f1(x)=|x-1|,f2(x)=$\frac{1}{3}$x+1,g(x)=$\frac{{f}_{1}(x)+{f}_{2}(x)}{2}$+$\frac{|{f}_{1}(x)-{f}_{2}(x)|}{2}$,
得g(x)=max{f(x1),f(x2)},作出函数g(x)的图象如图: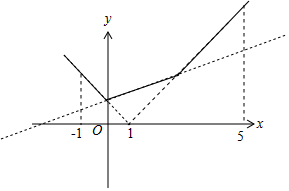
若a,b∈[-1,5],且当x1,x2∈[a,b](x1≠x2)时,$\frac{g({x}_{1})-g({x}_{2})}{{x}_{1}-{x}_{2}}$>0恒成立,
等价于函数g(x)为增函数,
由图可知,x∈[0,5],则(b-a)max=5.
故答案为:5.
点评 本题考查函数的值域及单调性,考查了数学转化思想方法和数形结合的解题思想方法,正确理解题意是解答该题的关键,是中档题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{17}{35}$ | C. | $\frac{1}{2}$ | D. | $\frac{9}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
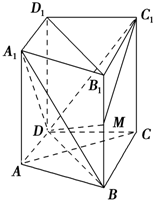 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1≤x≤3 | B. | x≤-1 | C. | x≥3 | D. | x<-1或x>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任意两条直线确定一个平面 | |
| B. | 三条平行直线最多确定三个平面 | |
| C. | 棱长为1的正方体的内切球的表面积为4π | |
| D. | 若平面α⊥平面β,平面β⊥平面γ,则平面α∥平面γ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com