
我们给出如下定义:对函数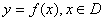 ,若存在常数
,若存在常数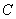 (
(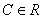 ),对任意的
),对任意的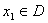 ,存在唯一的
,存在唯一的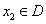 ,使得
,使得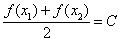 ,则称函数
,则称函数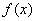 为“和谐函数”,称常数
为“和谐函数”,称常数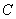 为函数
为函数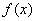 的 “和谐数”.
的 “和谐数”.
(Ⅰ)判断函数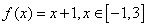 是否为“和谐函数”?答: . 是(填“是”或“否”)如果是,写出它的一个“和谐数”: .
是否为“和谐函数”?答: . 是(填“是”或“否”)如果是,写出它的一个“和谐数”: .
(Ⅱ)请先学习下面的证明方法:
证明:函数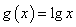 ,
,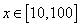 为“和谐函数”,
为“和谐函数”, 是其“和谐数”;
是其“和谐数”;
证明过程如下:对任意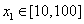 ,令
,令 ,即
,即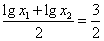 ,
,
得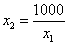 .∵
.∵ 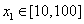 ,∴
,∴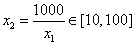 .
.
即对任意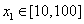 ,存在唯一的
,存在唯一的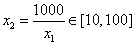 ,使得
,使得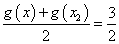 .
.
∴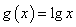 为“和谐函数”,其“和谐数”为
为“和谐函数”,其“和谐数”为 .
.
参照上述证明过程证明:函数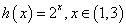 为“和谐函数”,
为“和谐函数”,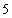 是其“和谐数”;
是其“和谐数”;
[证明]:
(III)判断函数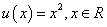 是否为和谐函数,并作出证明.
是否为和谐函数,并作出证明.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:
从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件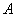 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率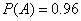 .
.
(Ⅰ)求从该批产品中任取1件是二等品的概率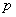 ;
;
(Ⅱ)若该批产品共20件,从中任意抽取2件,X表示取出的2件产品中二等品的件数,求X的分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com