Question

3．已知点M是圆C：（x+1）²+y²=1上的动点，定点D（1，0），点P在直线DM上，点N在直线CM上，且满足$\overrightarrow{DM}=2\overrightarrow{DP}$，$\overrightarrow{NP}•\overrightarrow{DM}=0$，动点N的轨迹是曲线E．
（1）求曲线E的方程；
（2）若AB是曲线E的长为2的动弦，O为坐标原点，求△AOB的面积S的最大值．

Answer 1

分析 （1）由条件可知NP为DM的中垂线，且CD＞CM，故而ND=NM，且|ND-NC|=1，故而可知N的轨迹为以C，D为焦点的双曲线，利用双曲线的定义求出方程；
（2）讨论直线AB的斜率，设出直线AB的方程，联立方程组，利用根的判别式、韦达定理、弦长公式、点到直线的距离公式，结合已知条件能求出△AOB面积S的最大值．

解答 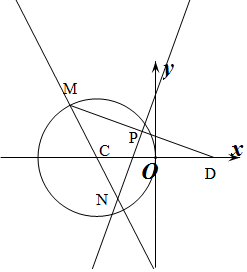解：（1）∵$\overrightarrow{DM}=2\overrightarrow{DP}$，$\overrightarrow{NP}•\overrightarrow{DM}=0$，
∴P是DM的中点，NP⊥DM，
∴ND=NM，
∴|ND-NC|=|NM-NC|=|CM|=1，
∴N点轨迹E为以C，D为焦点的双曲线，
设曲线E的方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$，则2a=1，c=1，
∴a²=$\frac{1}{4}$，b²=$\frac{3}{4}$．
∴曲线E的方程为$\frac{{x}^{2}}{\frac{1}{4}}-\frac{{y}^{2}}{\frac{3}{4}}=1$．
（2）当直线AB⊥x轴时，设A（a，1），则$\frac{{a}^{2}}{\frac{1}{4}}-\frac{1}{\frac{3}{4}}=1$，解得|a|=$\frac{\sqrt{21}}{6}$．
∴S_△OAB=$\frac{1}{2}×2×\frac{\sqrt{21}}{6}$=$\frac{\sqrt{21}}{6}$．
当直线AB方程为y=kx+b，
联立方程组$\left\{\begin{array}{l}{y=kx+b}\\{\frac{{x}^{2}}{\frac{1}{4}}-\frac{{y}^{2}}{\frac{3}{4}}=1}\end{array}\right.$，得（12-4k²）x²-8kbx-4b²-3=0，
设A（x₁，y₁），B（x₂，y₂），
则x₁+x₂=$\frac{2kb}{3-{k}^{2}}$，x₁x₂=$\frac{4{b}^{2}+3}{4{k}^{2}-12}$，
∵|AB|=2，∴$\sqrt{1+{k}^{2}}$$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=2，
即（1+k²）•[$\frac{4{k}^{2}{b}^{2}}{（3-{k}^{2}）^{2}}$-$\frac{4{b}^{2}+3}{{k}^{2}-3}$]=4，整理得：b²=$\frac{7{k}^{4}-30{k}^{2}+27}{12（1+{k}^{2}）}$，
由b²≥0得7k⁴-30k²+27≥0，解得0$≤{k}^{2}≤\frac{9}{7}$或k²≥3．
又点O到直线AB的距离h=$\frac{|b|}{\sqrt{1+{k}^{2}}}$，
∴S_△OAB=$\frac{1}{2}$|AB|•h=h，∴S²_△OAB=h²=$\frac{{b}^{2}}{1+{k}^{2}}$=$\frac{7{k}^{4}-30{k}^{2}+27}{12（1+{k}^{2}）^{2}}$=$\frac{7}{12}$-$\frac{11}{3（1+{k}^{2}）}$+$\frac{16}{3（1+{k}^{2}）^{2}}$，
令1+k²=t，则1≤t≤$\frac{16}{7}$或t≥4，设g（t）=$\frac{7}{12}$-$\frac{11}{3t}$+$\frac{16}{3{t}^{2}}$=$\frac{16}{3}$（$\frac{1}{t}$-$\frac{11}{32}$）²-$\frac{3}{64}$．
∵1≤t≤$\frac{16}{7}$或t≥4，∴$\frac{7}{16}$≤$\frac{1}{t}$≤1或0＜$\frac{1}{t}$≤$\frac{1}{4}$．
∴当$\frac{1}{t}$=1即t=1时，g（t）取得最大值g（1）=$\frac{9}{4}$，
此时S_△OAB=$\sqrt{g（1）}$=$\frac{3}{2}$，
∵$\frac{3}{2}$＞$\frac{\sqrt{21}}{6}$，
∴△AOB的面积S的最大值为$\frac{3}{2}$．

点评 本题考查了双曲线的定义，直线与双曲线的位置关系，解题时要注意根的判别式、韦达定理、弦长公式、点到直线的距离公式的合理运用．属于中档题．