
分析 设公比为q,由条件得:aq2-4aq+3a-1=0关于q∈R且q≠0有唯一解,由此能求出结果.
解答 解:设公比为q,
∵等比数列{an}满足:a1=a(a>0),${a_1}+1{,^{\;}}{a_2}+2{,^{\;}}{a_3}+3$成等比数列,
∴(aq+2)2=(a+1)(aq2+3),
整理,得:aq2-4aq+3a-1=0,
∵{an}唯一,∴由条件得:aq2-4aq+3a-1=0关于q∈R且q≠0有唯一解,
注意到a>0,△=16a2-4a(3a-1)>0恒成立,
∴3a-1=0,$a=\frac{1}{3}$(q=0为方程的增解).
故答案为:$\frac{1}{3}$.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{28}{3}$ | B. | $\frac{19}{2}$ | C. | 6 | D. | 2$\sqrt{10}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{5π}{6},\frac{7π}{6}]$ | B. | $[\frac{7π}{6},\frac{19π}{6}]$ | C. | $[-\frac{2π}{3},\frac{4π}{3}]$ | D. | $[-\frac{17π}{6},-\frac{5π}{6}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | [-1,2] | C. | {-1,0,1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>1 | B. | $m>\frac{1}{2}$ | C. | m>2 | D. | m≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
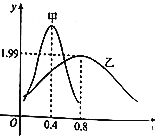 甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )| A. | 乙类水果的质量服从的正态分布的参数σ2=1.99 | |
| B. | 甲类水果的质量比乙类水果的质量更集中 | |
| C. | 甲类水果的平均质量μ1=0.4kg | |
| D. | 甲类水果的平均质量比乙类水果的平均质量小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com