
分析 根据正弦函数的图象和性质可得.
解答 解:函数y=sin(ωx-$\frac{π}{3}$)与y=$\frac{1}{2}$交点中距离最小为$\frac{π}{3}$,
∴sin(ωx-$\frac{π}{3}$)=$\frac{1}{2}$,
∴ωx1-$\frac{π}{3}$=2kπ+$\frac{π}{6}$,(1)
ωx2-$\frac{π}{3}$=2kπ+$\frac{5π}{6}$,(2)
(2)-(1)得:ω(x2-x1)=$\frac{2π}{3}$;
∵|x2-x1|=$\frac{π}{3}$,
∴ω•$\frac{π}{3}$=$\frac{2π}{3}$,
∴ω=2;
故答案为:2.
点评 本题考查三角函数的解析式的求法,注意三角函数的图象与性质的应用是解题的关键,考查计算能力,属于基础题,


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {(1,2)} | C. | {(2,1)} | D. | {(x,y)|x=1或y=2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向量$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{b}$垂直 | B. | 向量$\overrightarrow{a}-\overrightarrow{b}$与$\overrightarrow{a}$垂直 | ||
| C. | 向量$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}$垂直 | D. | 向量$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{a}-\overrightarrow{b}$平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 9 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
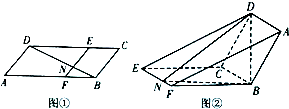 如图①,已知ABCD为平行四边形,∠A=60°,AF=2FB,AB=6,点E在CD上,EF∥BC,BD⊥AD,BD交EF于点N,现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上(如图②),则折后直线DN与直线BF所成角的余弦值为$\frac{{\sqrt{3}}}{4}$.
如图①,已知ABCD为平行四边形,∠A=60°,AF=2FB,AB=6,点E在CD上,EF∥BC,BD⊥AD,BD交EF于点N,现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上(如图②),则折后直线DN与直线BF所成角的余弦值为$\frac{{\sqrt{3}}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 16 | C. | 18 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com