
分析 ${a_{n+1}}=\left\{{\begin{array}{l}{2{a_n}}\\{{a_n}-1}\end{array}}\right.\begin{array}{l}{(0≤{a_n}≤1)}\\{({a_n}>1)}\end{array}$,且${a_1}=\frac{6}{7}$,可得an+5=an.利用周期性即可得出.
解答 解:∵${a_{n+1}}=\left\{{\begin{array}{l}{2{a_n}}\\{{a_n}-1}\end{array}}\right.\begin{array}{l}{(0≤{a_n}≤1)}\\{({a_n}>1)}\end{array}$,且${a_1}=\frac{6}{7}$,
∴a2=2a1=$\frac{12}{7}$,a3=a2-1=$\frac{5}{7}$,a4=2a3=$\frac{10}{7}$,a5=a4-1=$\frac{3}{7}$,a6=2a5=$\frac{6}{7}$,…,
∴an+5=an.
则a2017=a403×5+2=a2=$\frac{12}{7}$.
故答案为:$\frac{12}{7}$.
点评 本题考查了数列递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a=\sqrt{3}$ | B. | $a>\sqrt{3}$或$a<-\sqrt{3}$ | C. | $-\sqrt{3}<a<\sqrt{3}$ | D. | $-\sqrt{3}≤a≤\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | $2\sqrt{7}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
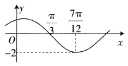 已知函数f(x)=Asin(wx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=Asin(wx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数的图象向左平移$\frac{π}{6}$个单位长度得到函数g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=2sin(2x-$\frac{π}{3}$) | B. | g(x)=2sin(2x+$\frac{π}{6}$) | C. | g(x)=-2sin(2x-$\frac{π}{3}$) | D. | g(x)=-2sin(2x+$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
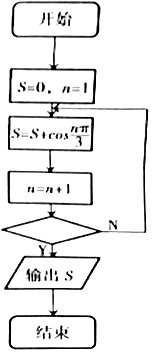 执行如图所示的程序框图,若输出S的值为-1,则判断框内,对于下列四个关于n的条件的选项,不能填入的是( )
执行如图所示的程序框图,若输出S的值为-1,则判断框内,对于下列四个关于n的条件的选项,不能填入的是( )| A. | n>3? | B. | n>5? | C. | n>32? | D. | n>203? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
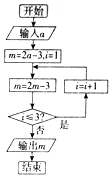 《九章算术》是中国古代数学名著,体现了古代劳动人民数学的智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出的m的值为35,则输入的a的值为( )
《九章算术》是中国古代数学名著,体现了古代劳动人民数学的智慧,其中第六章“均输”中,有一竹节容量问题,某教师根据这一问题的思想设计了如图所示的程序框图,若输出的m的值为35,则输入的a的值为( )| A. | 4 | B. | 5 | C. | 7 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com