
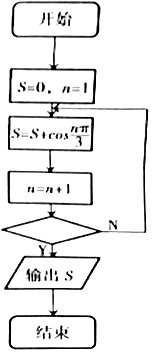
 执行如图所示的程序框图,若输出S的值为-1,则判断框内,对于下列四个关于n的条件的选项,不能填入的是( )
执行如图所示的程序框图,若输出S的值为-1,则判断框内,对于下列四个关于n的条件的选项,不能填入的是( )| A. | n>3? | B. | n>5? | C. | n>32? | D. | n>203? |
分析 由程序框图知:每次循环时计算出S的值,得出输出S的值为-1时,n=4k或n=4k+2,k∈Z时,
由此得判断框内可以填入的条件以及不能填入的条件.
解答 解:由程序框图知:第1次循环n=1,S=cos$\frac{π}{3}$=$\frac{1}{2}$;
第2次循环n=2,S=$\frac{1}{2}$+cos$\frac{2π}{3}$=0;
第3次循环n=3,S=0+cosπ=-1;
第4次循环n=4,S=-1+cos$\frac{4π}{3}$=-$\frac{3}{2}$;
第5次循环n=5,S=-$\frac{3}{2}$+cos$\frac{5π}{3}$=-1;
第6次循环n=6,S=-1+cos2π=0;
第7次循环n=7,S=0+cos$\frac{7π}{3}$=$\frac{1}{2}$;
…,∵输出的S的值为-1,
∴n=4k或n=4k+2,k∈Z时,终止循环体;
∴判断框内可以填入的条件是:n>3?或n>5?或n>203?,
不能填入n>32?.
故选:C.
点评 本题考查了循环结构的程序框图,根据流程依次计算程序运行的结果是解答此类问题的常用方法.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin(2x-\frac{π}{3}),x∈R$ | B. | $y=sin(\frac{x}{2}+\frac{π}{6}),x∈R$ | C. | $y=sin(2x+\frac{π}{3}),x∈R$ | D. | $y=sin(2x+\frac{2π}{3}),x∈R$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我国南宋时期的《数学九章》中提出了秦九韶算法来计算多项式的值,在执行下列算法的程序框图时,若输入的n=4,x=2,则输出V的值为( )
我国南宋时期的《数学九章》中提出了秦九韶算法来计算多项式的值,在执行下列算法的程序框图时,若输入的n=4,x=2,则输出V的值为( )| A. | 15 | B. | 31 | C. | 63 | D. | 127 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
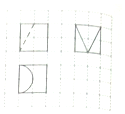 图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
图中,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | 8-$\frac{4}{3}$π | B. | 8-π | C. | 8-$\frac{2}{3}$π | D. | 8-$\frac{1}{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com