
| A. | [$\frac{9}{2}$-2$\sqrt{2}$,$\frac{9}{2}$+2$\sqrt{2}$] | B. | [$\frac{3}{2}$,$\frac{9}{2}$+2$\sqrt{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{9}{2}$-2$\sqrt{2}$,$\sqrt{2}$] |
分析 令t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],可得sinxcosx=$\frac{{t}^{2}-1}{2}$,y=$\frac{1}{2}$(t-2)2+$\frac{3}{2}$,再利用二次函数的性质求得它的值域.
解答 解:函数y=(sinx-2)(cosx-2)=sinx•cosx-2(sinx+cosx)+4,
令t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],可得sinxcosx=$\frac{{t}^{2}-1}{2}$,
y=$\frac{{t}^{2}-1}{2}$-2t+4=$\frac{1}{2}$(t2-4t+4)+$\frac{3}{2}$=$\frac{1}{2}$(t-2)2+$\frac{3}{2}$,
故当t=$\sqrt{2}$时,函数y取得最小值为$\frac{9}{2}$-2$\sqrt{2}$,当t=-$\sqrt{2}$时,函数y取得最大值为$\frac{9}{2}$+2$\sqrt{2}$,
故选:A.
点评 本题主要考查同角三角的基本关系,二次函数的性质,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -3+4i | B. | -3-4i | C. | 3+4i | D. | 3-4i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (0,3) | C. | (-5,4) | D. | (0,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
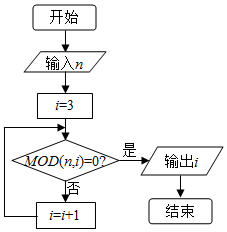 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
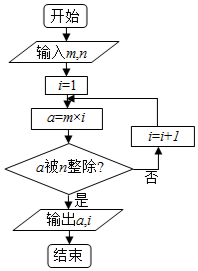 当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )
当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )| A. | 37${C}_{12}^{7}$ | B. | 38${C}_{12}^{8}$ | C. | -33${C}_{12}^{3}$ | D. | -37${C}_{12}^{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com