
【题目】已知函数![]() (
(![]() ,
, ![]() =2.718………),
=2.718………),
(I) 当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(II)当![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 恒成立,
恒成立,
求实数![]() 的最大值.
的最大值.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)符合题意的实数![]() 的最大值为
的最大值为![]() .
.
【解析】试题分析:(1)求函数单调区间,即求导研究导函数的正负,导函数大于零求增区间,导函数小于零求减区间;(2)这是不等式恒成立求参的问题,转化为![]() ,
, ![]() 对任意
对任意![]() 恒成立,再求导研究函数的单调性,求最值即可.
恒成立,再求导研究函数的单调性,求最值即可.
(1)![]()
由![]() 可知,
可知, ![]()
令![]() 得
得 ![]() 或
或![]()
令![]() 得
得 ![]()
即 此时函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)当![]() 时,不等式
时,不等式![]() 即
即 ![]()
令![]() ,
, ![]() 对任意
对任意![]() 恒成立
恒成立
又 ![]()
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上递增,且最小值为
上递增,且最小值为![]()
(i)当![]() ,即
,即![]() 时,
时, ![]() 对任意
对任意![]() 恒成立
恒成立
![]()
![]() 在
在![]() 上递增,
上递增, ![]() 当
当![]() 时,
时, ![]() 满足题意; (ii)当
满足题意; (ii)当![]() ,即
,即![]() 时,
时,
由上可得存在唯一的实数![]() ,使得
,使得![]() ,可得当
,可得当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递减,此时
上递减,此时![]() 不符合题意; 综上得,当
不符合题意; 综上得,当![]() 时,满足题意,即符合题意的实数
时,满足题意,即符合题意的实数![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,平面![]() 平面
平面![]() ,且四边形
,且四边形![]() 为矩形,四边形
为矩形,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
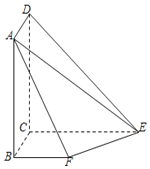
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的大小;
所成锐二面角的大小;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月,工信部颁发了国内首个![]() 无线电通信设备进网许可证,标志着
无线电通信设备进网许可证,标志着![]() 基站设备将正式接入公用电信商用网络.某
基站设备将正式接入公用电信商用网络.某![]() 手机生产商拟升级设备生产
手机生产商拟升级设备生产![]() 手机,有两种方案可供选择,方案1:直接引进
手机,有两种方案可供选择,方案1:直接引进![]() 手机生产设备;方案2:对已有的
手机生产设备;方案2:对已有的![]() 手机生产设备进行技术改造,升级到
手机生产设备进行技术改造,升级到![]() 手机生产设备.该生产商对未来
手机生产设备.该生产商对未来![]() 手机销售市场行情及回报率进行大数据模拟,得到如下统计表:
手机销售市场行情及回报率进行大数据模拟,得到如下统计表:
市场销售状态 | 畅销 | 平销 | 滞销 | |
市场销售状态概率 |
|
|
| |
预期年利润数值(单位:亿元) | 方案1 | 70 | 40 | -40 |
方案2 | 60 | 30 | -10 | |
(1)以预期年利润的期望值为依据,求![]() 的取值范围,讨论该生产商应该选择哪种方案进行设备升级?
的取值范围,讨论该生产商应该选择哪种方案进行设备升级?
(2)设该生产商升级设备后生产的![]()
![]() 万部,通过大数据模拟核算,选择方案1所生产的
万部,通过大数据模拟核算,选择方案1所生产的![]() 手机年度总成本
手机年度总成本![]() (亿元),选择方案2所生产的
(亿元),选择方案2所生产的![]() 手机年度总成为
手机年度总成为![]() (亿元).已知
(亿元).已知![]() ,当所生产的
,当所生产的![]() 手机市场行情为畅销、平销和滞销时,每部手机销售单价分别为0.8万元,
手机市场行情为畅销、平销和滞销时,每部手机销售单价分别为0.8万元,![]() (万元),
(万元),![]() (万元),根据(1)的决策,求该生产商所生产的
(万元),根据(1)的决策,求该生产商所生产的![]() 手机年利润期望的最大值?并判断这个年利润期望的最大值能否达到预期年利润数值.
手机年利润期望的最大值?并判断这个年利润期望的最大值能否达到预期年利润数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再把所得的函数图象上所有点的横坐标缩短到原来的
个单位长度,再把所得的函数图象上所有点的横坐标缩短到原来的![]() (纵坐标不变)得到函数
(纵坐标不变)得到函数![]() 的图象,关于
的图象,关于![]() 的说法有:①函数
的说法有:①函数![]() 的图象关于点
的图象关于点![]() 对称;②函数
对称;②函数![]() 的图象的一条对称轴是
的图象的一条对称轴是![]() ;③函数
;③函数![]() 在
在![]() 上的最上的最小值为
上的最上的最小值为![]() ;④函数
;④函数![]() 上单调递增,则以上说法正确的个数是( )
上单调递增,则以上说法正确的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的方程为
中,曲线C的方程为![]() ,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求直线l的直角坐标方程;
(2)已知P是曲线C上的一动点,过点P作直线![]() 交直线于点A,且直线
交直线于点A,且直线![]() 与直线l的夹角为45°,若
与直线l的夹角为45°,若![]() 的最大值为6,求a的值.
的最大值为6,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中.AB⊥BC,△PAC为等边三角形,二面角P﹣AC﹣B的余弦值为![]() ,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为( )
,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为( )
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .以原点为极点,
.以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com