【题目】在四棱锥
中，
底面
，底面为正方形，
，点
为正方形内部的一点，且
，则直线
与
所成角的余弦值的取值范围为( )
A.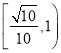
B.
C.
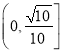D.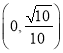
【答案】D
【解析】
根据题意，建立空间直角坐标系，在平面
上，由
计算
的轨迹方程，可知的轨迹是以
为圆心，以2为半径的圆，在正方形中的部分；根据平行找直线
与
所成角的平面角，根据的轨迹判定临界值，从而确定直线与所成角的余弦值的取值范围.
由题意，以
为坐标原点，分别以
为
轴，建立空间直角坐标系，如图所示，则有
，
设
，由，则列方程有
化简得
，即点的轨迹是以为圆心，以2为半径的圆，在正方形中的部分；
过作
垂足为
,连接
，则有
则直线与所成角的平面角为
，
则
根据点的轨迹是以为圆心，以2为半径的圆，在正方形中的部分，
则点轨迹与正方形的边交于一点
，记为
与正方形的
边交于一点
，记为
当点从运动到位置时，
逐渐减小，逐渐增大，则的取值逐渐减小，
计算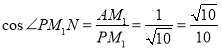
，
则直线与所成角的余弦值的取值范围是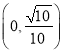
故选：
轻松夺冠全能掌控卷系列答案科目：高中数学 来源： 题型：
【题目】甲乙两人报名参加由某网络科技公司举办的“技能闯关”双人电子竞技比赛，比赛规则如下：每一轮“闯关”结果都采取计分制，若在一轮闯关中，一人过关另一人未过关，过关者得1分，未过关得
分；若两人都过关或都未过关则两人均得0分.甲、乙过关的概率分别为
和
，在一轮闯关中，甲的得分记为
.
（1）求的分布列；
（2）为了增加趣味性，系统给每位报名者基础分3分，并且规定出现一方比另一方多过关三轮者获胜，此二人比赛结束.
表示“甲的累积得分为
时，最终认为甲获胜”的概率，则
，其中
，
，
，令
.证明：点
的中点横坐标为
；
（3）在第（2）问的条件下求
，并尝试解释游戏规则的公平性.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
是递减的等差数列，的前
项和是
，且
，有以下四个结论：
①
；
②若对任意
都有
成立，则
的值等于7或8时；
③存在正整数，使
；
④存在正整数
，使
．
其中所有正确结论的序号是
A. ①②B. ①②③
C. ②③④D. ①②③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
，P是曲线上的动点，M为线段OP的中点，设点M的轨迹为曲线
．
（1）求的极坐标方程；
（2）若射线
与曲线异于极点的交点为A，与曲线异于极点的交点为B，求
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥
的底面是菱形，
底面
，
分别是
的中点，
，
，
.
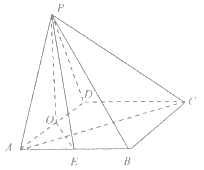
（I）证明：
；
（II）求直线
与平面
所成角的正弦值；
（III）在
边上是否存在点
，使
与
所成角的余弦值为
，若存在，确定点位置；若不存在，说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
