
【题目】点![]() 在圆
在圆![]() 上运动,
上运动,![]() 轴,
轴,![]() 为垂足,点
为垂足,点![]() 在线段
在线段![]() 上,满足
上,满足![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 作直线
作直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() 两点,使点
两点,使点![]() 为弦
为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由条件可知,点![]() 是
是![]() 的中点,所以根据求什么设什么的原则,设点
的中点,所以根据求什么设什么的原则,设点![]() ,则
,则![]() ,代入方程
,代入方程![]() ,可求得点
,可求得点![]() 的轨迹方程;(2)此题为直线与椭圆相交的中点弦问题,设直线方程为
的轨迹方程;(2)此题为直线与椭圆相交的中点弦问题,设直线方程为![]() ,与椭圆方程联立,根据韦达定理可得根与系数的关系,利用点
,与椭圆方程联立,根据韦达定理可得根与系数的关系,利用点![]() 是
是![]() 两点的中点,可求得直线的斜率,即得直线方程.
两点的中点,可求得直线的斜率,即得直线方程.
试题解析:(1)∵点![]() 在线段
在线段![]() 上,满足
上,满足![]() ,∴点
,∴点![]() 是线段
是线段![]() 的中点,
的中点,
设![]() ,则
,则![]() ,
,
∵点![]() 在圆
在圆![]() 上运动,则
上运动,则![]() ,即
,即![]() ,
,
∴点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)当直线![]() 轴时,由椭圆的对称性可得弦
轴时,由椭圆的对称性可得弦![]() 的中点在
的中点在![]() 轴上,不可能是点
轴上,不可能是点![]() ,这种情况不满足题意.
,这种情况不满足题意.
设直线![]() 的方程为
的方程为![]() ,
,
由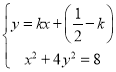 可得
可得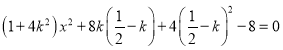 ,
,
由韦达定理可得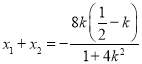 ,
,
由![]() 的中点为
的中点为![]() ,可得
,可得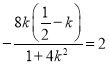 ,解得
,解得![]() ,
,
即直线![]() 的方程为
的方程为![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设某厂产品的次品率为2%,估算该厂8 000件产品中合格品的件数大约为( )
A. 160 B. 7 840
C. 7 998 D. 7 800
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)①当![]() 时,判断函数
时,判断函数![]() 的奇偶性并证明,并判断
的奇偶性并证明,并判断![]() 是否有上界,并说明理由;
是否有上界,并说明理由;
②若![]() ,函数
,函数![]() 在
在![]() 上的上界是
上的上界是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:“对于函数f(x),若存在x0,使f(x0)=x0成立,则称x0为函数f(x)的不动点。”已知f(x)=x2+bx+c.
(1)若f(x)有两个不动点为-3,2,求函数f(x)的零点.
(2)当c=![]() b2时,函数f(x)没有不动点,求实数b的取值范围.
b2时,函数f(x)没有不动点,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com