
| A. | (0,+∞) | B. | (-∞,-1)∪(0,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-1,+∞) |
分析 由已知条件构造辅助函数F(x)=$\frac{f(x)+2}{{e}^{2x}}$,求导,根据已知求得函数的单调区间,结合原函数的性质和函数值,即可f(x)>e2x-2的解集.
解答 解:由f(x)>e2x-2,得f(x)+2>e2x,得$\frac{f(x)+2}{{e}^{2x}}$>1,令F(x)=$\frac{f(x)+2}{{e}^{2x}}$,
则F′(x)=$\frac{f′(x){e}^{2x}-2[f(x)+2]{e}^{2x}}{({e}^{2x})^{2}}$=$\frac{f′(x)-2f(x)-4}{{e}^{2x}}$,
∵f′(x)-2f(x)-4>0,
∴F′(x)>0,
∴F(x)=$\frac{f(x)+2}{{e}^{2x}}$在R上单调递增,
f(0)=-1,F(0)=1,
∴原不等式等价于F(x)>F(0),
∴x>0,故不等式f(x)>e2x-2的解集为(0,+∞),
故答案选:A.
点评 本题考查函数的导数与单调性的结合,根据已知条件构造辅助函数,然后用导数判断函数的单调性是解题的关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | A=N+,B=N+,f:x→|x-3| | B. | A=N+,B={-1,1,-2},f:x→(-1)x | ||
| C. | A=Z,B=Q,f:x→$\frac{3}{x}$ | D. | A=N+,B=R,f:x→x的平方根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
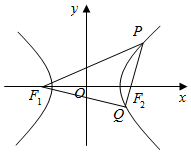 如图,F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,经过右焦点F2的直线与双曲线C的右支交于P,Q两点,且|PF2|=2|F2Q|,PQ⊥F1Q,则双曲线C的离心率是( )
如图,F1,F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,经过右焦点F2的直线与双曲线C的右支交于P,Q两点,且|PF2|=2|F2Q|,PQ⊥F1Q,则双曲线C的离心率是( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{10}}{2}$ | D. | $\frac{\sqrt{17}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com