
某商家一月份至五月份累计销售额达3 860万元,预测六月份销售额为500万元,七月份销售额比六月份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等.若一月份至十月份销售总额至少达7 000万元,则x的最小值是________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知f(x)为二次函数,且f(-1)=2,f ′(0)=0,
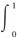 f(x)dx=-2.
f(x)dx=-2.
(1)求f(x)的解析式;
(2)求f(x)在[-1,1]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2x,x∈R.
(1)当m取何值时方程|f(x)-2|=m有一个解?两个解?
(2)若不等式f2(x)+f(x)-m>0在R上恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变,假设在放射性回位素铯137的衰变过程中,其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:M(t)=M02 ,其中M0为t=0时铯137的含量,已知t=30时,铯137含量的变化率是-10 ln 2(太贝克/年),则M(60)=( )
,其中M0为t=0时铯137的含量,已知t=30时,铯137含量的变化率是-10 ln 2(太贝克/年),则M(60)=( )
A.5 太贝克 B.75 ln 2太贝克
C.150 ln 2太贝克 D.150 太贝克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com