练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝2x，x∈R.

    (1)当m取何值时方程|f(x)－2|＝m有一个解？两个解？

    (2)若不等式f2(x)＋f(x)－m>0在R上恒成立，求m的取值范围．


    解：

    (1)令F(x)＝|f(x)－2|＝|2x－2|，G(x)＝m，画出F(x)的图象如图所示：

    由图象看出，当m＝0或m≥2时，函数F(x)与G(x)的图象只有一个交点，原方程有一个解；

    当0<m<2时，函数F(x)与G(x)的图象有两个交点，原方程有两个解．

    (2)令f(x)＝t(t>0)，H(t)＝t2＋t，

    ∵H(t)＝－在区间(0，＋∞)上是增函数，

    ∴H(t)>H(0)＝0，因此要使t2＋t>m在区间(0，＋∞)上恒成立，应有m≤0，即所求m的取值范围为(－∞，0]．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设则a、b、c的大小关系为(　　)

    A．a>b>c  B．b>a>c  C．a>c>b  D．b>c>a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝loga(x＋1)－loga(1－x)，a>0且a≠1.

    (1)求f(x)的定义域；

    (2)判断f(x)的奇偶性并予以证明；

    (3)当a>1时，求使f(x)>0的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知关于x的方程|x2－6x|＝a(a>0)的解集为P，则P中所有元素的和可能是(　　)

    A．3,6,9  B．6,9,12  C．9,12,15  D．6,12,15

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)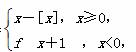＝其中[x]表示不超过x的最大整数，如[－1.5]＝－2，[1.5]＝1，若直线y＝k(x＋1)(k>0)与函数y＝f(x)的图象有三个不同的交点，则k的取值范围是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在一次数学实验中，运用计算器采集到如下一组数据：

    x

    －2.0

    －1.0

    0

    1.0

    2.0

    3.0

    y

    0.24

    0.51

    1

    2.02

    3.98

    8.02

    则x、y的函数关系与下列哪类函数最接近(其中a、b为待定系数)(　　)

    A．y＝a＋bx　B．y＝a＋bx　C．y＝ax2＋b　D．y＝a＋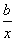

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某商家一月份至五月份累计销售额达3 860万元，预测六月份销售额为500万元，七月份销售额比六月份递增x%，八月份销售额比七月份递增x%，九、十月份销售总额与七、八月份销售总额相等．若一月份至十月份销售总额至少达7 000万元，则x的最小值是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点P是△ABC所在平面内的一点，边AB的中点为D，若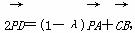，其中λ∈R，则P点一定在(　　)

    A．AB边所在的直线上                     B．BC边所在的直线上

    C．AC边所在的直线上                     D．△ABC的内部

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    复数z满足z(1－i)＝2i，则复数z的实部与虚部之和为(　　)

    A．－2                                  B．2 

    C．1                                    D．0

    查看答案和解析>>

    同步练习册答案