
| A. | 1 | B. | 37 | C. | 100 | D. | -37 |
分析 根据等比数列的性质和通项公式进行求解即可.
解答 解:∵数列{an},{bn}都是等比数列,
∴设数列{an},{bn}的公比分别为q,p,
则当n≥2时,$\frac{{a}_{n}•{b}_{n}}{{a}_{n-1}•{b}_{n-1}}$=pq为常数,
即么数列{an•bn}也是等比数列,
∵a1=25,b1=4,a2•b2=100,
∴数列{an•bn}的公比pq=$\frac{{a}_{2}{b}_{2}}{{a}_{1}{b}_{1}}$=$\frac{100}{25×4}=1$,
则数列{an•bn}的第37项等于a2•b2=100,
故选:C
点评 本题主要考查等比数列的判断以及等比数列通项公式的应用,根据等比数列的性质判断数列{an•bn}也是等比数列是解决本题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
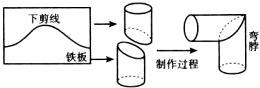 铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图,当弯脖的直径为12cm时,a应是6cm.
铁匠师傅在打制烟筒弯脖时,为确保对接成直角,在铁板上的下剪线正好是余弦曲线$y=acos\frac{x}{a}$的一个周期的图象如图,当弯脖的直径为12cm时,a应是6cm.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
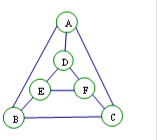 执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.
执行某个程序,电脑会随机地按如下要求给图中六个小圆涂色.| A. | $\frac{9}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{18}{25}$ | D. | $\frac{12}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com