练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在(x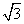－)10的展开式中，x6的系数是________．


    1 890

    解析：Tr＋1＝Cx10－r(－)r，令10－r＝6，r＝4，T5＝9Cx6＝1 890x6.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)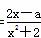＝在区间[－1，1]上是增函数．

    (1) 求实数a的值组成的集合A；

    (2) 设x1、x2是关于x的方程f(x)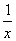＝的两个相异实根，若对任意a∈A及t∈[－1，1]，不等式m2＋tm＋1≥|x1－x2|恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设x∈N＋， 求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用五种不同颜色给图中四个区域涂色，每个区域涂一种颜色．

    (1) 共有多少种不同的涂色方法？

    (2) 若要求相邻(有公共边)的区域不同色，那么有多少种不同的涂色方法？

    1

    2

    3

    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从1，3，5，7，9这五个数中，每次取出两个不同的数分别为a，b，共可得到lga－lgb的不同值的个数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果的展开式中，第四项和第七项的二项式系数相等，求：

    (1) 展开式的中间项；

    (2) 展开式中所有的有理项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知(2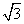－x)50＝a0＋a1x＋a2x2＋…＋a50x50，其中a0，a1，a2…，a50是常数，计算(a0＋a2＋a4＋…＋a50)2－(a1＋a3＋a5＋…＋a49)2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知盒中有10个灯泡，其中8个正品，2个次品．需要从中取出2只正品，每次取一个，取出后不放回，直到取出2个正品为止．设X为取出的次数，求X的概率分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ和η，且ξ、η分布列为

    ξ

    1

    2

    3

    P

    a

    0.1

    0.6

    　　

    η

    1

    2

    3

    P

    0.3

    b

    0.3

    (1) 求a、b的值；

    (2) 计算ξ、η的期望和方差，并以此分析甲、乙的技术状况．

    查看答案和解析>>

    同步练习册答案