Question

11．函数f（x）=$\sqrt{{（x+3）}^{2}+16}$+$\sqrt{{（x-5）}^{2}+4}$的值域为[10，+∞）．

Answer 1

分析 由$\sqrt{{（x+3）}^{2}+16}$+$\sqrt{{（x-5）}^{2}+4}$的几何意义，即动点M（x，0）与两定点A（-3，4）、B（5，2）的距离和求得答案．

解答 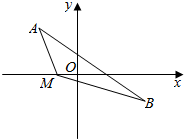解：f（x）=$\sqrt{{（x+3）}^{2}+16}$+$\sqrt{{（x-5）}^{2}+4}$=$\sqrt{[x-（-3）]^{2}+（0-4）^{2}}+\sqrt{（x-5）^{2}+（0+2）^{2}}$，
其几何意义为动点M（x，0）与两定点A（-3，4）、B（5，-2）的距离和，
如图，
∵|AB|=$\sqrt{（-3-5）^{2}+（4+2）^{2}}=10$，且|MA|+|MB|≥|AB|，
∴f（x）=$\sqrt{{（x+3）}^{2}+16}$+$\sqrt{{（x-5）}^{2}+4}$≥10．
故答案为：[10，+∞）．

点评 本题考查函数值域的求法，考查了数形结合的解题思想方法和数学转化思想方法，是中档题．