练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．如图，两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，那么①AD⊥MN；②MN∥平面CDE；③MN∥CE；④MN、CE异面．其中假命题的个数为（　　）
    A．4B．3C．2D．1

    分析 取AD的中点G，连接MG，NG，结合正方形的性质，我们结合线面垂直的判定定理及性质可判断①的真假；连接AC，CE，根据三角形中位线定理，及线面平行的判定定理，可以判断②③④的真假，进而得到答案

    解答 解：∵两个正方形ABCD和ADEF所在平面互相垂直，M、N分别是BD和AE的中点，
    取AD的中点G，连接MG，NG，易得AD⊥平面MNG，进而得到AD⊥MN，故①正确；
    连接AC，CE，根据三角形中位线定理，可得MN∥CE，由线面平行的判定定理，可得②MN∥面CDE及③MN∥CE正确，④MN、CE错误；
    ∴其中假命题的个数为：1
    故选：D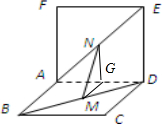

    点评 本题考查了平面与平面垂直的性质，直线与平面垂直的判定及直线与平面平行的判定，熟练掌握空间直线与平面平行及垂直的判定及性质是解答本题的关键．属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．已知sin（π+α）-3cos（2π-α）=0，则cos2α的值为（　　）
    A．$\frac{4}{5}$B．-$\frac{4}{5}$C．$\frac{3}{5}$D．-$\frac{3}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知复数z在复平面内对应的点为（1，2），则|$\overline{z}$+i|=$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．某市统计局就本地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（每个分组包括左端点，不包括右短点，如第一组表示月收入在[1000，1500）（单位：元）

    （Ⅰ）估计居民月收入在[1500，2000）的概率
    （Ⅱ）根据频率分布直方图估计样本数据的众数、中位数
    （Ⅲ）统计方法中．同一组数据常用该组区间的中点值作为代表，据此估计样本数据的平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知角θ∈（0，π），有实数S，6sinθ+4Scosθ=5S，求S的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．若方程ln（k-ex）+x-1=0有解，求k的最小值2$\sqrt{e}$．

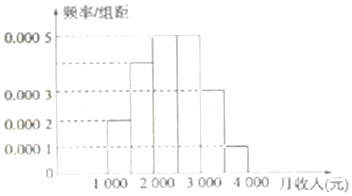
    查看答案和解析>>

    科目：高中数学 来源：2017届陕西汉中城固县高三10月调研数学（文）试卷（解析版） 题型：选择题

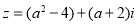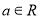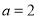    已知复数（），则“”是“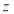为纯虚数”的（ ）

    A．充分不必要条件

    B．必要不充分条件

    C．既不充分也不必要条件

    D．充要条件

    查看答案和解析>>

    科目：高中数学 来源：2017届陕西汉中城固县高三10月调研数学（理）试卷（解析版） 题型：选择题

    某几何体的三视图如图所示，图中的四边形都是边长为2的正方形，正视图和侧视图中的两条虚线都互相垂直且相等，则该几何体的体积是（ ）

    A． B．

    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若函数f（x）=x3-2ax2+a在（a-1，a+$\frac{1}{2}$）上有最大值，则正数a的取值范围为 （　　）
    A．（0，1）B．[$\frac{1}{2}$，1）C．（0，$\frac{1}{2}$]D．（$\frac{1}{2}，\frac{3}{2}$）

    查看答案和解析>>

    同步练习册答案