
分析 由方程ln(k-ex)+x-1=0有解,可得k=ex+e1-x,对ex+e1-x,运用基本不等式即可得到所求最小值.
解答 解:ln(k-ex)+x-1=0,
即有ln(k-ex)=1-x,
k-ex=e1-x,
即为k=ex+e1-x,
由ex+e1-x≥2$\sqrt{{e}^{x}•{e}^{1-x}}$=2$\sqrt{e}$,
当且仅当ex=e1-x,即x=$\frac{1}{2}$时,取得等号.
则方程ln(k-ex)+x-1=0有解,
k的最小值为2$\sqrt{e}$,
故答案为:2$\sqrt{e}$.
点评 本题考查方程有解的条件,注意运用分离参数法,考查转化思想和基本不等式的运用:求最值,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(文)试卷(解析版) 题型:选择题
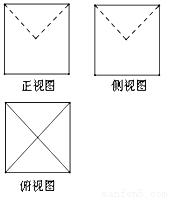
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN、CE异面.其中假命题的个数为( )
如图,两个正方形ABCD和ADEF所在平面互相垂直,设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN、CE异面.其中假命题的个数为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源:2017届陕西汉中城固县高三10月调研数学(理)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系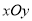 中,直线
中,直线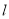 的参数方程为
的参数方程为 (
(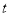 为参数),以原点
为参数),以原点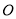 为极点,
为极点,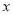 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线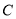 的极坐标方程为
的极坐标方程为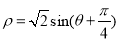 .
.
(1)求曲线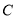 的直角坐标方程;
的直角坐标方程;
(2)若直线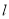 与曲线
与曲线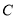 交于
交于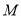 ,
,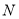 两点,求
两点,求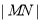 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com