练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)＝x3＋3ax2＋bx＋a2在x＝－1时有极值0，则a－b的值为________．


    －7

    [解析]　f ′(x)＝3x2＋6ax＋b，若在x＝－1处有极值0，则

    解得但当a＝1，b＝3时，f ′(x)＝3(x＋1)2≥0，不合题意，

    故a－b＝－7.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知数列中，a1＝1，a2＝2＋3，a3＝4＋5＋6，a4＝7＋8＋9＋10，…，则a10＝(　　)

    A．610       B．510       C．505       D．750

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二次函数y＝f(x)的图象过原点，且它的导函数y＝f ′(x)的图象是过第一、二、三象限的一条直线，则函数y＝f(x)的图象的顶点在(　　)

    A．第一象限  B．第二象限

    C．第三象限  D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3－px2－qx的图象与x轴切于(1,0)点，则f(x)的极大值、极小值分别为(　　)

    A.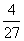，0                                                      B．0，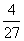

    C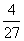．－，0                                                D．0，－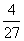

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝ax3－2ax2＋b(a≠0)．

    (1)求出f(x)的极值；

    (2)若f(x)在区间[－2,1]上最大值是5，最小值是－11，求f(x)的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)＝lnx＋ax(a∈R且a≠0)．

    (1)讨论函数f(x)的单调性；

    (2)若a＝1，证明：x∈[1,2]时，f(x)－3<成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的函数f(x)满足(x＋2)f ′(x)<0(其中f ′(x)是函数f(x)的导数)，又a＝f(log3)，b＝f[(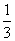)0.1]，c＝f(ln3)，则a，b，c的大小关系为______．(从大到小排列)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某工厂生产某种儿童玩具，每件玩具的成本价为30元，并且每件玩具的加工费为t元(其中t为常数，且2≤t≤5)，设该工厂每件玩具的出厂价为x元(35≤x≤41)，根据市场调查，日销售量与ex(e为自然对数的底数)成反比例，当每件玩具的出厂价为40元时，日销售量为10件．

    (1)求该工厂的日利润y(元)与每件玩具的出厂价x元的函数关系式；

    (2)当每件玩具的日售价为多少元时，该工厂的利润y最大，并求y的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


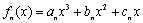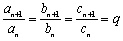
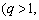
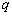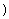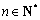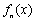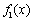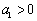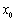    已知函数，满足为常数，，给出下列说法：①函数为奇函数；②若函数在R上单调递增，则；③若是函数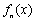的极值点，则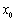也是函数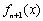的极值点；④若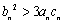，则函数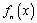在R上有极值．以上说法正确的个数是

    A．4             B．3           C．2                D．1　

    查看答案和解析>>

    同步练习册答案