
定义在R上的函数f(x)满足(x+2)f ′(x)<0(其中f ′(x)是函数f(x)的导数),又a=f(log 3),b=f[(
3),b=f[(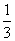 )0.1],c=f(ln3),则a,b,c的大小关系为______.(从大到小排列)
)0.1],c=f(ln3),则a,b,c的大小关系为______.(从大到小排列)
科目:高中数学 来源: 题型:
已知函数f(x)= (k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
(k为常数,e=2.71828…是自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
(1)求k的值;
(2)求f(x)的单调区间;
(3)设g(x)=(x2+x)f ′(x),其中f ′(x)为f(x)的导函数,证明:对任意x>0,g(x)<1+e-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
某公司生产某种产品,固定成本为20000元,每生产一单位产品,成本增加100元,已知总收益R与产量x的关系是R=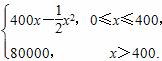 则总利润最大时,每年生产的产品产量是( )
则总利润最大时,每年生产的产品产量是( )
A.100 B.150
C.200 D.300
查看答案和解析>>
科目:高中数学 来源: 题型:
一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度v(t)=7-3t+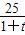 (t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )
(t的单位:s,v的单位:m/s)行驶至停止.在此期间汽车继续行驶的距离(单位:m)是( )
A.1+25ln5 B.8+25ln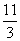
C.4+25ln5 D.4+50ln2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知在平面直角坐标系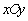 中,圆
中,圆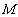 的方程为
的方程为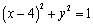 .以原点
.以原点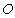 为极点,以
为极点,以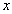 轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线
轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线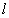 的极坐标方程为
的极坐标方程为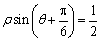 .
.
(Ⅰ)求直线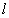 的直角坐标方程和圆
的直角坐标方程和圆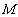 的参数方程;
的参数方程;
(Ⅱ)求圆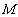 上的点到直线
上的点到直线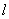 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com