
分析 (1)代入求值即可;
(2)用定义法,先看定义域是否关于原点对称,再研究f(-x)与f(x)的关系.若相等,则为偶函数;若相反,则为奇函数.
解答 解:(1)∵f(2)=$\frac{2×2}{{2}^{2}-1}$=$\frac{4}{3}$,
∴f[f(2)]=$\frac{2×\frac{4}{3}}{(\frac{4}{3})^{2}-1}$=$\frac{24}{7}$;
(2)f(x)是奇函数.理由如下:
∵f(x)=$\frac{2x}{{x}^{2}-1}$的定义域是x≠±1.
又f(-x)=$\frac{-2x}{(-x)^{2}-1}$=-$\frac{2x}{{x}^{2}-1}$,即f(-x)=-f(x),
∴f(x)是奇函数.
点评 本题主要考查函数奇偶性的判断,函数的值.证明函数的寄偶性时,一般用定义.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
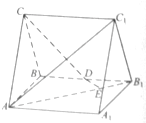 如图,直三棱柱ABC-A1B1C1中,AC=BC,AA1=AB,D为BB1的中点,E为AB1上的一点,AE=3EB1.
如图,直三棱柱ABC-A1B1C1中,AC=BC,AA1=AB,D为BB1的中点,E为AB1上的一点,AE=3EB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | $\frac{1}{9}$ | C. | $-\frac{7}{9}$ | D. | $-\frac{1}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com