练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

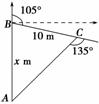
    如图，在日本地震灾区的搜救现场，一条搜救狗从A处沿正北方向行进x m到达B处发现一个生命迹象，然后向右转105°，进行10 m到达C处发现另一生命迹象，这时它向右转135°后继续前行回到出发点，那么x＝________.


     m

    解析　由题知，∠CBA＝75°，∠BCA＝45°，∴∠BAC＝180°－75°－45°＝60°，∴＝.

    ∴x＝ m.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f(x)＝sin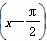 (x∈R)，下面结论错误的是(　　)．

    A．函数f(x)的最小正周期为2π

    B．函数f(x)在区间上是增函数

    C．函数f(x)的图象关于直线x＝0对称

    D．函数f(x)是奇函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝sinωx＋sin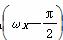，x∈R.

    (1)若ω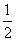＝，求f(x)的最大值及相应的x的集合；

    (2)若x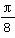＝是f(x)的一个零点，且0<ω<10，求ω的值和f(x)的最小正周期．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，内角A，B，C的对边分别为a，b，c，且bsinA=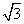acosB.

    （1）求角B的大小；

    （2）若b=3，sinC=2sinA，求a，c的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    据新华社报道，强台风“珍珠”在广东饶平登陆．台风中心最大风力达到12级以上，大风降雨给灾区带来严重的灾害，不少大树被大风折断．某路边一树干被台风吹断后，折成与地面成45°角，树干也倾斜为与地面成75°角，树干底部与树尖着地处相距20米，则折断点与树干底部的距离是(　　)．

    　　　　　　　　　　　　　　　　　　　

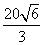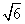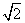    A.米         B．10米        C.米         D．20米

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上．在小艇出发时，轮船位于港口O北偏西30°且与该港口相距20海里的A处，并正以30海里/时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v海里/时的航行速度匀速行驶，经过t小时与轮船相遇．

    (1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

    (2)假设小艇的最高航行速度只能达到30海里/时，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    查看答案和解析>>

    科目：高中数学 来源： 题型：


     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}：1，－，，－，…的一个通项公式是(　　)

    查看答案和解析>>

    同步练习册答案