从边长为4的正方形ABCD内部任取一点P.则P到对角线AC的距离不大于$\sqrt{2}$的概率为$\frac{3}{4}$．题目和参考答案——青夏教育精英家教网—

15．从边长为4的正方形ABCD内部任取一点P，则P到对角线AC的距离不大于$\sqrt{2}$的概率为$\frac{3}{4}$．

分析根据题意，画出正方形ABCD，求出满足条件的点P所在的区域面积，由几何概型的概率公式，即可求出对应的概率．

解答解：如图所示，
E、F、G、H分别为AD、DC、AB和BC的中点，
点P落在阴影部分所在的区域，
由几何概型的概率公式，
得所求的概率为P=1-$\frac{\frac{1}{2}×2×2×2}{4×4}$=$\frac{3}{4}$．
故答案为：$\frac{3}{4}$．

点评本题考查了几何概型的概率计算问题，解题的关键是得出概率的计算公式是对应面积的比值，是基础题目．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

7．已知a∈R，方程a²x²+（a+2）y²+4x+8y+5a=0表示圆，则圆心坐标是（-2，-4），半径是5．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

6．

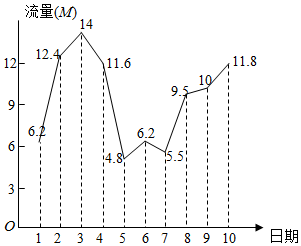小王的手机使用的是每月300M流量套餐，如图记录了小王在4月1日至4月10日这十天的流量使用情况，下列叙述中正确的是（　　）

	A．	1日-10日这10天的平均流量小于9.0M/日
	B．	11日-30日这20天，如果每天的平均流量不超过11M，这个月总流量就不会超过套餐流量
	C．	从1日-10日这10天的流量中任选连续3天的流量，则3日，4日，5日这三天的流量的方差最大
	D．	从1日-10日这10天中的流量中任选连续3天的流量，则8日，9日，10日这三天的流量的方差最小

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

3．设α是锐角，若sin（α+$\frac{π}{3}$）=$\frac{4}{5}$+sinα，则cos（2α-$\frac{π}{6}$）=（　　）

A．

$\frac{12}{25}$

B．

$\frac{24}{25}$

C．

-$\frac{24}{25}$

D．

-$\frac{12}{25}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．若a=2^0.5，b=log_π3，c=log₂sin$\frac{2π}{5}$，则a、b、c从小到大的顺序是c＜b＜a．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

20．设数列数列{b_n}满足b_n+1=$\frac{1}{2}$b_n+$\frac{1}{4}$，且b₁=$\frac{7}{2}$，T_n为{b_n}的前n项和．
（1）求证：数列{b_n-$\frac{1}{2}$}是等比数列并求数列{b_n}的通项公式；
（2）如果对任意n∈N^*，不等式$\frac{2{T}_{n}+3•{2}^{2-n}-10}{k}$≤n²+4n+5若恒成立，求实数k的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

7．在区间[0，$\frac{3π}{4}$]上随机取一个数x，则时间“sinx+cosx≥1”发生的概率为（　　）

A．

$\frac{1}{4}$

B．

$\frac{1}{3}$

C．

$\frac{1}{2}$

D．

$\frac{2}{3}$

查看答案和解析>>