
分析 先利用诱导公式,将两个三角函数式中的角化到同一个单调区间,结合余弦函数的单调性,可得两个函数值的大小.
解答 解:(1)cos(-$\frac{23}{5}$π)=cos(-$\frac{3}{5}$π)=cos($\frac{3}{5}$π),
cos(-$\frac{17}{4}$π)=cos(-$\frac{1}{4}$π)=cos($\frac{1}{4}$π),
由余弦函数在[0,π]上为减函数可得:cos($\frac{3}{5}$π)<cos($\frac{1}{4}$π),
即cos(-$\frac{23}{5}$π)<cos(-$\frac{17}{4}$π);
(2)sin194°=-sin14°=-cos76°,
cos160°=-cos20°,
由余弦函数在[0°,180°]上为减函数可得:cos76°<cos20°,
∴sin194°>cos160°.
点评 本题考查的知识点是三角函数诱导公式和余弦函数的单调性,难度中档.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:解答题
| 年份x年 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
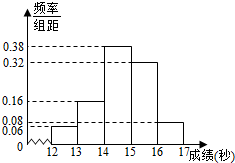 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
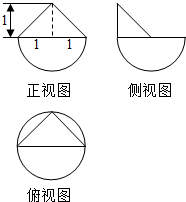 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 3π+2$\sqrt{2}$-1 | B. | 3π+2$\sqrt{2}$ | C. | 2π+2$\sqrt{2}$-1 | D. | 2π+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
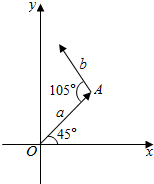 在直角坐标系中,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$如图所示,求它们的坐标.
在直角坐标系中,|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$,$\overrightarrow{b}$如图所示,求它们的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com