
【题目】据《人民网》报道,美国国家航空航天局(NASA)发文称,相比20年前世界变得更绿色了,卫星资料显示中国和印度的行动主导了地球变绿.据统计,中国新增绿化面积的![]() 来自于植树造林,下表是中国十个地区在去年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
来自于植树造林,下表是中国十个地区在去年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
单位:公顷
地区 | 造林总面积 | 造林方式 | ||||
人工造林 | 飞播造林 | 新封山育林 | 退化林修复 | 人工更新 | ||
内蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 13507 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
重庆 | 226333 | 100600 | 62400 | 63333 | ||
陕西 | 297642 | 184108 | 33602 | 63865 | 16067 | |
甘肃 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
宁夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012 | 4000 | 3999 | 1053 | |
(1)请根据上述数据分别写出在这十个地区中人工造林面积与造林总面积的比值最大和最小的地区;
(2)在这十个地区中,任选一个地区,求该地区新封山育林面积占造林总面积的比值超过![]() 的概率;
的概率;
(3)在这十个地区中,从退化林修复面积超过一万公顷的地区中,任选两个地区,记X为这两个地区中退化林修复面积超过六万公顷的地区的个数,求X的分布列及数学期望.
【答案】(1)人工造林面积与总面积比最大的地区为甘肃省,人工造林面积与总面积比最小的地区为青海省;(2)![]() ;(3)分布列见详解,数学期望为
;(3)分布列见详解,数学期望为![]()
【解析】
(1)通过数据的观察以及计算人工造林面积与造林总面积比值,可得结果.
(2)通过数据的观察以及计算新封山育林面积与造林总面积比值,得出比值超过![]() 的地区个数,然后可得结果.
的地区个数,然后可得结果.
(3)计算退化林修复面积超过一万公顷的地区中选两个地区总数![]() ,退化林修复面积超过六万公顷的地区的个数为
,退化林修复面积超过六万公顷的地区的个数为![]() ,列出
,列出![]() 所有取值并计算相应概率,然后可得结果.
所有取值并计算相应概率,然后可得结果.
(1)人工造林面积与总面积比最大的地区为甘肃省,
人工造林面积与总面积比最小的地区为青海省.
(2)记事件A:在这十个地区中,任选一个地区,该地区
新封山育林面积占总面积的比值超过![]()
根据数据可知:青海地区人工造林面积占总面积比超过![]() ,
,
则![]()
(3)退化林修复面积超过一万公顷有6个地区:
内蒙、河北、河南、重庆、陕西、新疆,
其中退化林修复面积超过六万公顷有3个地区:
内蒙、河北、重庆,
所以X的取值为0,1,2
所以![]() ,
,![]() ,
,
![]()
随机变量X的分布列如下:
|
|
|
|
|
|
|
|
![]()


科目:高中数学 来源: 题型:
【题目】设函数![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,以
,以![]() 为切点作函数
为切点作函数![]() 图象的切线交
图象的切线交![]() 轴于点
轴于点![]() ,再过
,再过![]() 作
作![]() 轴的垂线
轴的垂线![]() 交函数
交函数![]() 图象于点
图象于点![]() ,
,![]() ,以此类推得点
,以此类推得点![]() ,记
,记![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)证明数列![]() 为等比数列并求出通项公式;
为等比数列并求出通项公式;
(2)设直线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,记
,记![]() (其中
(其中![]() 为坐标原点),求数列
为坐标原点),求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某中学学生对《中华人民共和国交通安全法》的了解情况,调查部门在该校进行了一次问卷调查(共12道题),从该校学生中随机抽取40人,统计了每人答对的题数,将统计结果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如下频率分布直方图.
六组,得到如下频率分布直方图.
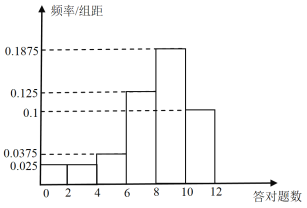
(1)若答对一题得10分,未答对不得分,估计这40人的成绩的平均分(同一组中的数据用该组区间的中点值作代表);
(2)若从答对题数在![]() 内的学生中随机抽取2人,求恰有1人答对题数在
内的学生中随机抽取2人,求恰有1人答对题数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户考察了一款热销的净水器,使用寿命为十年,过滤由核心部件滤芯来实现.在使用过程中,滤芯需要不定期更换,其中滤芯每个200元.如图是根据100台该款净水器在十年使用期内更换的滤芯的件数制成的柱状图.(以100台净水器更换滤芯的频率代替1台净水器更换滤芯发生的概率)
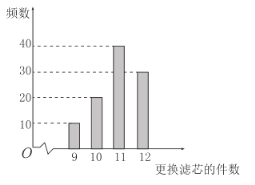
(1)估计一台净水器在使用期内更换滤芯的件数的众数和中位数.
(2)估计一台净水器在使用期内更换滤芯的件数大于10的概率.
(3)已知上述100台净水器在购机的同时购买滤芯享受5折优惠(使用过程中如需再购买无优惠),假设每台净水器在购机的同时购买滤芯10个,这100台净水器在使用期内,更换滤芯的件数记为a,所需费用记为y,补全下表,估计这100台净水器在使用期内购买滤芯所需总费用的平均数.
100台该款净水器在试用期内更换滤芯的件数a | 9 | 10 | 11 | 12 |
频数 | ||||
费用y |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:从数列{an}中抽取m(m∈N,m≥3)项按其在{an}中的次序排列形成一个新数列{bn},则称{bn}为{an}的子数列;若{bn}成等差(或等比),则称{bn}为{an}的等差(或等比)子数列.
(1)记数列{an}的前n项和为Sn,已知![]() .
.
①求数列{an}的通项公式;
②数列{an}是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由.
(2)已知数列{an}的通项公式为an=n+a(a∈Q+),证明:{an}存在等比子数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,线段
,线段![]() 的长为4.点
的长为4.点![]() 在椭圆
在椭圆![]() 上且位于第一象限,过点
上且位于第一象限,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
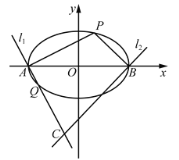
(1)若点![]() 的横坐标为-1,求点
的横坐标为-1,求点![]() 的坐标;
的坐标;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点为
的另一交点为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ;
;
②函数![]() 有2个零点;
有2个零点;
③![]() 的解集为
的解集为![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 和
和![]() ,由4个点
,由4个点![]() 、
、![]() 、
、![]() 和
和![]() 组成了一个高为
组成了一个高为![]() ,面积为
,面积为![]() 的等腰梯形.
的等腰梯形.
(1)求椭圆的方程;
(2)过点![]() 的直线和椭圆交于两点
的直线和椭圆交于两点![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com