
设 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有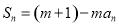
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比
的公比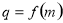 ,数列
,数列 满足
满足
 ,
,
 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前 项和
项和 .
.
(1)详见解析;(2)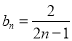 ;(3)
;(3)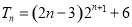
【解析】
试题分析:(1)用公式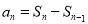
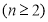 将
将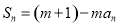 化简可得
化简可得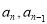 间的关系,根据等比数列的定义可证得数列
间的关系,根据等比数列的定义可证得数列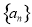 是等比数列。(2)属构造法求数列通项公式:因为
是等比数列。(2)属构造法求数列通项公式:因为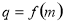
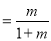 ,所以
,所以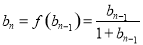 ,将其取倒数可推导出
,将其取倒数可推导出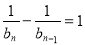 ,根据等差数列的定义可知
,根据等差数列的定义可知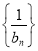 为等差数列,先求
为等差数列,先求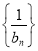 的通项公式,再求
的通项公式,再求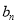 。(3)因为
。(3)因为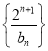 得通项公式为等差乘以等比数列所以应用错位相减法求数列的前
得通项公式为等差乘以等比数列所以应用错位相减法求数列的前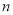 项和。将
项和。将 表示为各项的和,然后将上式两边同时乘以通项公式里边等比数列的公比,但应将第一位空出,然后两式相减即可。
表示为各项的和,然后将上式两边同时乘以通项公式里边等比数列的公比,但应将第一位空出,然后两式相减即可。
试题解析:(1)证明:当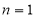 时,
时,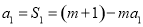 ,解得
,解得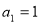 . 1分
. 1分
当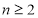 时,
时, .即
.即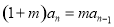 2分
2分
∵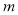 为常数,且
为常数,且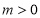 , ∴
, ∴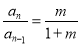
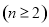 . 3分
. 3分
∴数列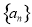 是首项为1,公比为
是首项为1,公比为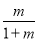 的等比数列. 4分
的等比数列. 4分
(2)【解析】
由(1)得,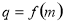
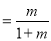 ,
,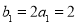 .
.
∵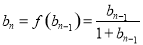 , ∴
, ∴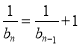 ,即
,即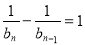
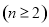 . 7分
. 7分
∴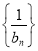 是首项为
是首项为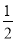 ,公差为1的等差数列. 8分
,公差为1的等差数列. 8分
∴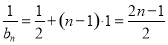 ,即
,即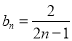 (
(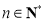 ). 9分
). 9分
(3)【解析】
由(2)知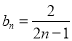 ,则
,则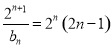 . 10分
. 10分
所以 ,
,
即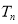
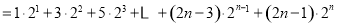 , ①
, ①
则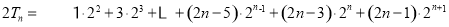 ②
②
②-①得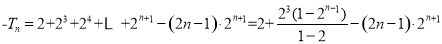 ,
,
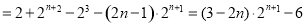
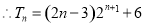 . 14分
. 14分
考点:1等比数列的定义;2等差数列的定义及通项公式;3错位相减法求数列的和。


科目:高中数学 来源:2015届江苏扬州市高二第一学期期末调研考试数学试卷(解析版) 题型:填空题
若 是三条互不相同的空间直线,
是三条互不相同的空间直线,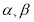 是两个不重合的平面,
是两个不重合的平面,
则下列命题中为真命题的是 (填所有正确答案的序号).
①若 则
则 ; ②若
; ②若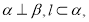 则
则 ;
;
③若 则
则 ; ④若
; ④若 则
则
查看答案和解析>>
科目:高中数学 来源:2015届广东阳东广雅、阳春实验中学高二上期末文数学卷(解析版) 题型:选择题
已知p:函数f(x)=x2+mx+1有两个零点,q:?x∈R,4x2+4(m-2)x+1>0.若p∧?q为真,则实数m的取值范围为( ).
A.(2,3) B.(-∞,1]∪(2,+∞)
C.(-∞,-2)∪[3,+∞) D.(-∞,-2)∪(1,2]
查看答案和解析>>
科目:高中数学 来源:2015届广东省等七校高二2月联考理科数学试卷(解析版) 题型:选择题
某种商品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据,根据表中提供的全部数据,用最小二乘法得出
(单位:万元)之间有如下对应数据,根据表中提供的全部数据,用最小二乘法得出 与
与 的线性回归方程为
的线性回归方程为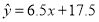 ,则表中的
,则表中的 的值为( )
的值为( )

A.45 B.50 C.55 D.60
查看答案和解析>>
科目:高中数学 来源:2015届广东省等七校高二2月联考文科数学试卷(解析版) 题型:选择题
执行如右图所示的程序框图.则输出的所有点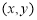 都在函数( )的图象上.
都在函数( )的图象上.
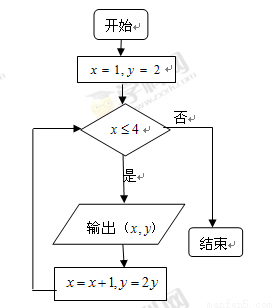
A. 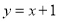 B.
B. 
C. 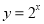 D.
D. 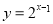
查看答案和解析>>
科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末理科数学试卷(解析版) 题型:选择题
在棱长为1的正方体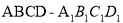 中,
中,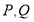 分别为线段
分别为线段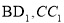 上的动点,则
上的动点,则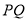 的最小值为( )
的最小值为( )
A. 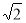 B.
B.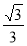 C.
C. 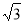 D.
D.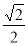
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com