解:(1)因为2S
n=a
na
n+1;所以n=1时2S
1=a
1•a
2,a
1=1,所以a
2=2,
∵2S
n=a
na
n+1;∴2S
n+1=a
n+1a
n+2;
可得2a
n+1=a
n+1a
n+2-a
na
n+1;
∵a
n>0∴a
n+2-a
n=2;
∵a
1=1,a
2=2,
∴数列{a
n}是等差数列,
a
n=n.
(2)数列{b
n}是首项和公比都等于2的等比数列,所以b
n=2
n,数列{a
nb
n}的前n项和
S
n=a
1b
1+a
2b
2+…+a
nb
n=1×2+2×2
2+…+n×2
n…①
2S
n=1×2
2+2×2
3+…+(n-1)×2
n+n×2
n+1…②
所以②-①得
S
n=n×2
n+1-(2+2
2+…+2
n)=(n-1)2
n+1+2.
(3)证明∵f(n)=
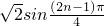
,
T
n=
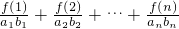
=
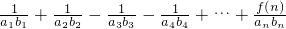
,
T
1=
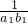
=

,T
2=
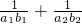
=
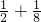
=

,
当n≥3时T
n=
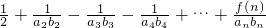
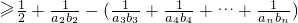
≥
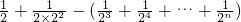
=
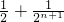

又T
n=
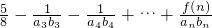
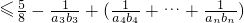
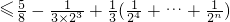
=
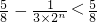
综上
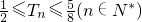
分析:(1)通过2S
n=a
na
n+1;推出数列的递推关系式,推出数列是等差数列,然后求数列{a
n}的通项公式;
(2)通过数列{b
n}是首项和公比都等于2的等比数列,求出b
n,利用错位相减法求解数列{a
nb
n}的前n项和.
(3)通过f(n)=
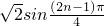
,化简T
n=
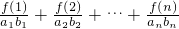
的表达式,求出T
1,T
2,当n≥3时转化T
n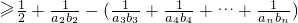
,与T
n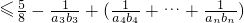
,然后证明
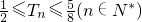
.
点评:本题考查等差数列与等比数列综合应用,数列与不等式的综合应用,考查数列求和的方法,考查分析问题解决问题的能力.

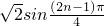 ,Tn=
,Tn=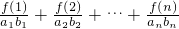 ,求证:
,求证: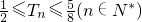 .
.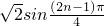 ,
,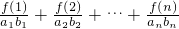
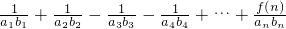 ,
,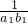 =
= ,T2=
,T2=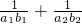 =
=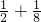 =
= ,
,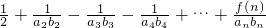
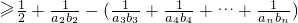
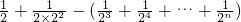
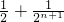

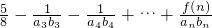
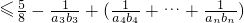
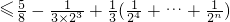
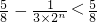
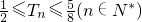
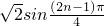 ,化简Tn=
,化简Tn=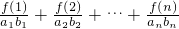 的表达式,求出T1,T2,当n≥3时转化Tn
的表达式,求出T1,T2,当n≥3时转化Tn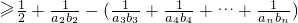 ,与Tn
,与Tn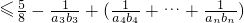 ,然后证明
,然后证明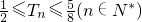 .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案