
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(Ⅰ)求证AM//平面BDE;
(Ⅱ)求二面角A-DF-B的大小;
(Ⅲ)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
(1)对于线面平行的证明,主要是分析借助于中位线来得到AM∥OE
(2)60º(3)P是AC的中点
解析试题分析:解法一: (1)记AC与BD的交点为O,连接OE, ∵O、M分别是AC、EF的中点, ACEF是矩形,∴四边形AOEM是平行四边形,
∴AM∥OE.∵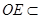 平面BDE,
平面BDE, 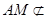 平面BDE,∴AM∥平面BDE.……4分
平面BDE,∴AM∥平面BDE.……4分
(2)在平面AFD中过A作AS⊥DF于S,连结BS,∵AB⊥AF, AB⊥AD, 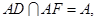 ∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
∴AB⊥平面ADF,∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF.∴∠BSA是二面角A—DF—B的平面角.
在RtΔASB中,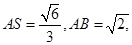
∴ ∴二面角A—DF—B的大小为60º.……8分
∴二面角A—DF—B的大小为60º.……8分
(3)设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,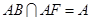 ,∴PQ⊥平面ABF,
,∴PQ⊥平面ABF,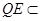 平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.
平面ABF,∴PQ⊥QF.在RtΔPQF中,∠FPQ=60º,PF=2PQ.
∵ΔPAQ为等腰直角三角形,∴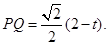 又∵ΔPAF为直角三
又∵ΔPAF为直角三
角形,∴ ,∴
,∴ 所以t=1或t=3(舍去),即点P是AC的中点.……12分
所以t=1或t=3(舍去),即点P是AC的中点.……12分
解法二: (1)建立空间直角坐标系.
设 ,连接NE, 则点N、E的坐标分别是(
,连接NE, 则点N、E的坐标分别是(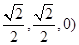 、(0,0,1),
、(0,0,1),
∴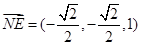 , 又点A、M的坐标分别是
, 又点A、M的坐标分别是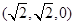 ,(
,(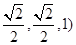
∴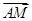 =(
=(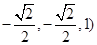 ∴
∴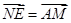 且NE与AM不共线,∴NE∥AM.又∵
且NE与AM不共线,∴NE∥AM.又∵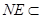 平面BDE,
平面BDE, 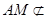 平面BDE,∴AM∥平面BDE.
平面BDE,∴AM∥平面BDE.
(2)∵AF⊥AB,AB⊥AD,AF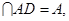 ∴AB⊥平面ADF.
∴AB⊥平面ADF.
∴
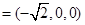 为平面DAF的法向量.
为平面DAF的法向量.
∵ =(
=(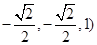 ·
· =0,
=0,
∴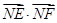 =(
=(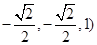 ·
·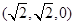 =0得
=0得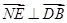 ,
,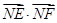 ,∴NE为平面BDF的法向量.
,∴NE为平面BDF的法向量.
∴cos<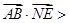 =
=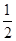 ∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.
∴AB与NE的夹角是60º.即所求二面角A—DF—B的大小是60º.
(3)设P(t,t,0)(0≤t≤ )得
)得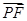
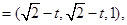 ∴
∴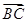 =(0,
=(0,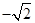 , 0)
, 0)
又∵PF和BC所成的角是60º.∴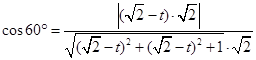
解得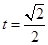 或
或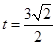 (舍去),即点P是AC的中点.
(舍去),即点P是AC的中点.
考点:空间中线面的位置关系
点评:解决的关键是根据线面平行的判定定理,以及空间的法向量来求解二面角的平面角的大小,属于中档题。


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
在图一所示的平面图形中, 是边长为
是边长为  的等边三角形,
的等边三角形, 是分别以
是分别以 为底的全等的等腰三角形,现将该平面图形分别沿
为底的全等的等腰三角形,现将该平面图形分别沿 折叠,使
折叠,使 所在平面都与平面
所在平面都与平面 垂直,连接
垂直,连接 ,得到图二所示的几何体,据此几何体解决下面问题.
,得到图二所示的几何体,据此几何体解决下面问题.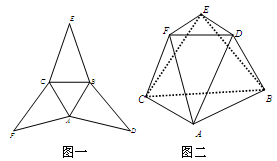
(1)求证: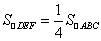 ;
;
(2)当 时,求三棱锥
时,求三棱锥 的体积
的体积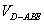 ;
;
(3)在(2)的前提下,求二面角 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(理科)如图分别是正三棱台ABC-A1B1C1的直观图和正视图,O,O1分别是上下底面的中心,E是BC中点.
(1)求正三棱台ABC-A1B1C1的体积;
(2)求平面EA1B1与平面A1B1C1的夹角的余弦;
(3) 若P是棱A1C1上一点,求CP+PB1的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,BE = BC = 1,AE =  ,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点。
(1)求证:MN⊥EA;
(2)求四棱锥M – ADNP的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
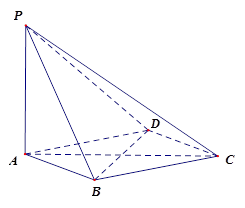
在四棱锥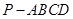 中,
中,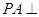 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形,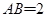 ,
,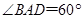 .
.
(1)求证: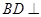 平面PAC;
平面PAC;
(2)若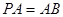 ,求PB与AC所成角的余弦值;
,求PB与AC所成角的余弦值;
(3)若PA=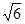 ,求证:平面PBC⊥平面PDC
,求证:平面PBC⊥平面PDC
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=2,OB=3,OC=4,E是OC的中点.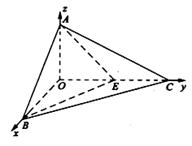
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A-BE-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com