
(本小题满分10分)选修4—1: 几何证明选讲
如图,直线 经过
经过 ⊙O上一点
⊙O上一点 ,且
,且 ,
,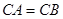 ,⊙O交直线
,⊙O交直线 于
于 .
.
(1)求证:直线 是⊙O的切线;
是⊙O的切线;
(2)若 ⊙O的半径为3,求
⊙O的半径为3,求 的长.
的长.
(Ⅰ)见解析(Ⅱ)5
解析试题分析:(Ⅰ)如图,连接OC,
∵ OA=OB,CA=CB,∴ OC⊥AB,∴ AB是⊙O的切线
(Ⅱ)∵ ED是直径, ∴ ∠ECD=90°,Rt△BCD中,
∵ tan∠CED=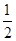 , ∴
, ∴ 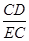 =
=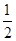 , ∵ AB是⊙O的切线,
, ∵ AB是⊙O的切线,
∴ ∠BCD=∠E,又 ∵ ∠CBD=∠EBC,∴ △BCD∽△BEC,
∴ 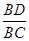 =
=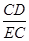 =
=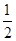 , 设BD=x,则BC=2x,
, 设BD=x,则BC=2x,
又BC2=BD·BE, ∴  =x·( x+6),
=x·( x+6),
解得:x1=0,x2=2, ∵ BD=x>0, ∴ BD=2, ∴ OA=OB=BD+OD=3+2=5?
考点:平面几何的证明计算
点评:应用圆中的知识点及直线与圆相切相交的线段长度关系推理计算


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
如图,在边长为1的等边△ABC中,D、E分别为边AB、AC上的点,若A关于直线DE的对称点A1恰好在线段BC上,
(1)①设A1B=x,用x表示AD;②设∠A1AB=θ∈[0º,60º],用θ表示AD
(2)求AD长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于HH,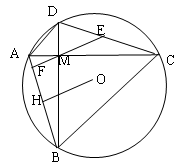
求证:(1)EF⊥AB (2)OH=ME
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修41:几何证明选讲
如图,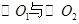 相交于A、B两点,AB是
相交于A、B两点,AB是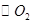 的直径,过A点作
的直径,过A点作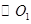 的切线交
的切线交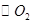 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与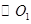 、
、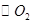 交于C,D两点.
交于C,D两点.
求证:(1)PA·PD=PE·PC; (2)AD=AE.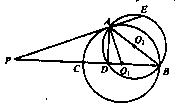
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
((本小题满分10分)选修4—1:几何证明选讲
如图,已知AD是 的外角
的外角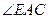 的平分线,交BC的延长线于点D,延长DA交
的平分线,交BC的延长线于点D,延长DA交 的外接圆于点F,连结FB、FC
的外接圆于点F,连结FB、FC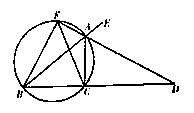
(I)求证:FB=FC;
(II)求证:FB2=FA·FD;
(III)若AB是 外接圆的直径,
外接圆的直径,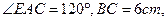 求AD的长。
求AD的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com