练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知， 其中是常数且，若的最小值是，满足条件的点是椭圆一弦的中点，则此弦所在的直线方程为（　　）

    A. B. C. D.

    【答案】B

    【解析】∵sm、n、s、t为正数，m+n=3， ，s+t的最小值是，

    ∴（s+t）（）的最小值 是，

    ∴（s+t）（）=m+n，满足时取最小值，

    此时最小值为m+n+2=3+2，得：mn=2，又：m+n=3，所以，m=1，n=2．

    设以（1，2）为中点的弦交椭圆于A（x1，y1），B（x2，y2），

    由中点坐标公式知x1+x2=2，y1+y2=4，

    把A（x1，y1），B（x2，y2）分别代入4x2+y2=16，

    得

    两式相减得2（x1﹣x2）+（y1﹣y2）=0，

    ∴k= ∴此弦所在的直线方程为y﹣2=﹣2（x﹣1），

    即2x+y﹣4=0．

    故答案为：B。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】我市“金牛”公园欲在长、宽分别为 、的矩形地块内开凿一“挞圆”形水池（如图），池边由两个半椭圆和（）组成，其中，“挞圆”内切于矩形且其左右顶点， 和上顶点构成一个直角三角形．

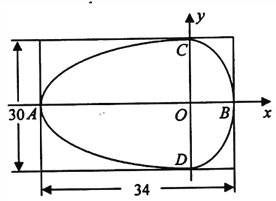
    （1）试求“挞圆”方程；

    （2）若在“挞圆”形水池内建一矩形网箱养殖观赏鱼，则该网箱水面面积最大为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的离心率为 ，其左顶点A在圆O：x2+y2=16上． （Ⅰ）求椭圆W的方程；
    （Ⅱ）若点P为椭圆W上不同于点A的点，直线AP与圆O的另一个交点为Q．是否存在点P，使得 ？若存在，求出点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】集合{x|cos（πcosx）=0，x∈[0，π]}=（用列举法表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系上，有一点列P0 ， P1 ， P2 ， P3 ， …，Pn﹣1 ， Pn ， 设点Pk的坐标（xk ， yk）（k∈N，k≤n），其中xk、yk∈Z，记△xk=xk﹣xk﹣1 ， △yk=yk﹣yk﹣1 ， 且满足|△xk||△yk|=2（k∈N* ， k≤n）；
    （1）已知点P0（0，1），点P1满足△y1＞△x1＞0，求P1的坐标；
    （2）已知点P0（0，1），△xk=1（k∈N* ， k≤n），且{yk}（k∈N，k≤n）是递增数列，点Pn在直线l：y=3x﹣8上，求n；
    （3）若点P0的坐标为（0，0），y2016=100，求x0+x1+x2+…+x2016的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．若g（x）存在2个零点，则a的取值范围是

    A. [–1，0） B. [0，+∞） C. [–1，+∞） D. [1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】.函数f（x）=ex+x2+x+1与g（x）的图象关于直线2x﹣y﹣3=0对称，P，Q分别是函数f（x），g（x）图象上的动点，则|PQ|的最小值为__

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设二次函数满足条件：

    （1）当时，且；

    （2）当时，；

    （3）在R上的最小值为0.

    求最大的m（m>1）,使得存在,只要，就有

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}定义为a1＞0，a11=a，an+1=an+ an2 ， n∈N*
    （1）若a1= （a＞0），求 + +…+ 的值；
    （2）当a＞0时，定义数列{bn}，b1=ak（k≥12），bn+1=﹣1+ ，是否存在正整数i，j（i≤j），使得bi+bj=a+ a2+ ﹣1．如果存在，求出一组（i，j），如果不存在，说明理由．

    查看答案和解析>>

    同步练习册答案