
| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
分析 由数列递推式求出a3,结合a20=a16求得a16,然后由an+2=$\frac{1}{{{a_n}+1}}$,可得a16=a2,则答案可求.
解答 解:由a1=1,an+2=$\frac{1}{{{a_n}+1}}$,得${a}_{3}=\frac{1}{{a}_{1}+1}=\frac{1}{2}$.
${a}_{20}=\frac{1}{{a}_{18}+1}=\frac{1}{\frac{1}{{a}_{16}+1}+1}={a}_{16}$,
即${{a}_{16}}^{2}+{a}_{16}-1=0$.
∵an>0,∴${a}_{16}=\frac{-1+\sqrt{5}}{2}$.
则由an+2=$\frac{1}{{{a_n}+1}}$及${a}_{16}=\frac{-1+\sqrt{5}}{2}$求得${a}_{2}=\frac{-1+\sqrt{5}}{2}$.
∴a2+a3=$\frac{-1+\sqrt{5}}{2}+\frac{1}{2}=\frac{\sqrt{5}}{2}$.
故选:B.
点评 本题考查了数列递推式,解答此题的关键是对数列规律性的发现,是中档题.


科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
已知椭圆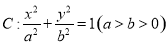 的左、右焦点分别为
的左、右焦点分别为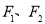 ,椭圆
,椭圆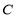 过点
过点 ,直线
,直线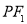 交
交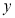 轴于
轴于 ,且
,且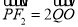 ,
,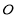 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)设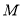 是椭圆
是椭圆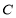 的上顶点,过点
的上顶点,过点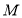 分别作直线
分别作直线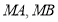 交椭圆
交椭圆 于
于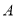 ,
,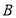 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线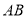 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,1) | B. | .(-∞,-1)∪(0,1) | C. | (-1,0)∪(1,+∞) | D. | (-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com