
分析 (2)由(1)得:f(x)+f(1-x)=1,进而可得f($\frac{1}{101}$)+f($\frac{2}{101}$)+…+f($\frac{100}{101}$)=50[f(x)+f(1-x)].
解答 解::∵函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$.
∴1-f(1-x)=1-$\frac{{4}^{1-x}}{{4}^{1-x}+2}$=$\frac{{4}^{1-x}+2-{4}^{1-x}}{{4}^{1-x}+2}$=$\frac{2}{{4}^{1-x}+2}$=$\frac{{4}^{x}}{{4}^{x}+2}$=f(x),
得:f(x)+f(1-x)=1,
∴f($\frac{1}{101}$)+f($\frac{2}{101}$)+…+f($\frac{100}{101}$)=50[f($\frac{1}{101}$)+f(1-$\frac{1}{101}$)]=50.
故答案为:50.
点评 本题考查的知识点是函数的对称性,其中熟练掌握函数对称变换法则,是解答的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北邢台市高一上学期月考一数学试卷(解析版) 题型:选择题
设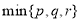 为表示
为表示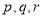 三者中较小的一个, 若函数
三者中较小的一个, 若函数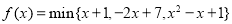 ,则不等式
,则不等式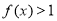 的解集为( )
的解集为( )
A.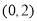 B.
B.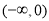
C.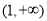 D.
D.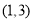
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)在第一象限的部分与过点A(2,0)、B(0,1)的直线相切于点T,且椭圆的离心率e=$\frac{\sqrt{3}}{2}$.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)在第一象限的部分与过点A(2,0)、B(0,1)的直线相切于点T,且椭圆的离心率e=$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com