
分析 (1)根据椭圆的性质及等差数列性质得出a=$\sqrt{2}$c,把P点坐标代入椭圆方程列方程组解出a,b得出椭圆方程;
(2)设Q(m,0),讨论直线l的斜率,求出A,B坐标,列方程解出m.
解答 解:(1)∵$\sqrt{2}$|PF1|,|F1F2|,$\sqrt{2}$|PF2|成等差数列,
∴$\sqrt{2}$|PF1|+$\sqrt{2}$|PF2|=2|F1F2|,即2$\sqrt{2}$a=4c,∴a=$\sqrt{2}c$.
∴$\left\{\begin{array}{l}{a=\sqrt{2}c}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\sqrt{2}}\\{b=1}\\{c=1}\end{array}\right.$.
∴椭圆方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(2)假设在x轴上存在点Q(m,0),使得$\overrightarrow{QA}•\overrightarrow{QB}=-\frac{7}{16}$恒成立.
①当直线l的斜率为0时,A(-$\sqrt{2}$,0),B($\sqrt{2}$,0).
∴$\overrightarrow{QA}$=(-$\sqrt{2}$-m,0),$\overrightarrow{QB}$=($\sqrt{2}$-m,0).
∴$\overrightarrow{QA}•\overrightarrow{QB}$=m2-2=-$\frac{7}{16}$,解得$m=\frac{5}{4}$或m=-$\frac{5}{4}$.
②若直线l无斜率,则A(1,$\frac{\sqrt{2}}{2}$),B(1,-$\frac{\sqrt{2}}{2}$),
∴$\overrightarrow{QA}$=(1-m,$\frac{\sqrt{2}}{2}$),$\overrightarrow{QB}$=(1-m,-$\frac{\sqrt{2}}{2}$),
∴$\overrightarrow{QA}•\overrightarrow{QB}$=(1-m)2-$\frac{1}{2}$=-$\frac{7}{16}$,解得m=$\frac{5}{4}$或m=$\frac{3}{4}$.
③若直线l斜率不为0,设直线AB的方程为x=ty+1.
联立方程组$\left\{\begin{array}{l}{x=ty+1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,消元得:(t2+2)y2+2ty-1=0.
设A(x1,y1),B(x2,y2),则y1+y2=-$\frac{2t}{{t}^{2}+2}$,y1y2=-$\frac{1}{{t}^{2}+2}$.
∴x1+x2=t(y1+y2)+2=$\frac{4}{{t}^{2}+2}$,
x1x2=(ty1+1)(ty2+1)=t2y1y2+t(y1+y2)+1=$\frac{-2{t}^{2}+2}{{t}^{2}+2}$.
∵$\overrightarrow{QA}$=(x1-m,y1),$\overrightarrow{QB}$=(x2-m,y2).
∴$\overrightarrow{QA}•\overrightarrow{QB}$=(x1-m)(x2-m)+y1y2=x1x2-m(x1+x2)+m2+y1y2
=$\frac{-2{t}^{2}+2}{{t}^{2}+2}$-$\frac{4m}{{t}^{2}+2}$+m2-$\frac{1}{{t}^{2}+2}$=$\frac{({m}^{2}-2){t}^{2}+2{m}^{2}-4m+1}{{t}^{2}+2}$=-$\frac{7}{16}$.
∴$\left\{\begin{array}{l}{-2+{m}^{2}=-\frac{7}{16}}\\{2{m}^{2}-4m+1=-\frac{7}{8}}\end{array}\right.$,解得m=$\frac{5}{4}$.
综上,Q点坐标为($\frac{5}{4}$,0).
点评 本题考查椭圆的定义及方程、直线与椭圆的位置关系、属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
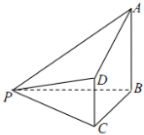 如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2.
如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{29}{36}$ | B. | $\frac{31}{44}$ | C. | $\frac{36}{55}$ | D. | $\frac{43}{66}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com