
【题目】已知函数![]() ,
,![]() 。
。
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调性。
的单调性。
【答案】(Ⅰ)a=3;(Ⅱ)答案见解析.
【解析】
(Ⅰ)先求出f(x)的导数f′(x),再根据![]() ,即可求得
,即可求得![]() 的值;
的值;
(Ⅱ)由题意可知,f(x)的定义域为(0,+∞),![]() ,令f′(x)=0,得x1=1,x2=a1.据此分类讨论函数的单调性即可.
,令f′(x)=0,得x1=1,x2=a1.据此分类讨论函数的单调性即可.
(Ⅰ)由题意可得:![]() ,故
,故![]() ,∴
,∴![]() .
.
(Ⅱ)∵函数![]() ,其中a>1,
,其中a>1,
∴f(x)的定义域为(0,+∞),![]() ,
,
令f′(x)=0,得x1=1,x2=a1.
①若a1=1,即a=2时,![]() ,故f(x)在(0,+∞)单调递增.
,故f(x)在(0,+∞)单调递增.
②若0<a1<1,即1<a<2时,
由f′(x)<0得,a1<x<1;
由f′(x)>0得,0<x<a1,或x>1.
故f(x)在(a1,1)单调递减,在(0,a1),(1,+∞)单调递增.
③若a1>1,即a>2时,
由f′(x)<0得,1<x<a1;由f′(x)>0得,0<x<1,或x>a1.
故f(x)在(1,a1)单调递减,在(0,1),(a1,+∞)单调递增.
综上可得,当a=2时,f(x)在(0,+∞)单调递增;
当1<a<2时,f(x)在(a1,1)单调递减,在(0,a1),(1,+∞)单调递增;
当a>2时,f(x)在(1,a1)单调递减,在(0,1),(a1,+∞)单调递增.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,设直线
,设直线![]() ,其中
,其中![]() ,给出下列结论:
,给出下列结论:
①直线![]() 的方向向量与向量
的方向向量与向量![]() 共线;
共线;
②若![]() ,则直线
,则直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ;
;
③直线![]() 与直线
与直线![]() (
(![]() )一定平行;
)一定平行;
写出所有真命题的序号________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点分别为
的两焦点分别为![]() ,
,![]() ,
,![]() 是椭圆在第一象限内的一点,并满足
是椭圆在第一象限内的一点,并满足![]() ,过
,过![]() 作倾斜角互补的两直线
作倾斜角互补的两直线![]() 、
、![]() 分别交椭圆于
分别交椭圆于![]() 、
、![]() 两点.
两点.
(1)求![]() 点坐标;
点坐标;
(2)当直线![]() 经过点
经过点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为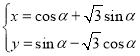 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
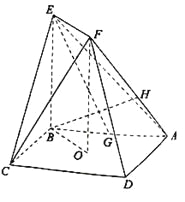
(Ⅰ)求证:EG∥平面ADF;
(Ⅱ)求二面角OEFC的正弦值;
(Ⅲ)设H为线段AF上的点,且AH=![]() HF,求直线BH和平面CEF所成角的正弦值.
HF,求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】诚信是立身之本,道德之基,某校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一个周期 |
|
|
|
|
第二个周期 |
|
|
|
|
第三个周期 |
|
|
|
|
(1)计算表中十二周“水站诚信度”的平均数![]() ;
;
(2)分别从表中每个周期的4个数据中随机抽取1个数据,设随机变量![]() 表示取出的3个数中“水站诚信度”超过
表示取出的3个数中“水站诚信度”超过![]() 的数据的个数,求随机变量
的数据的个数,求随机变量![]() 的分布列和期望;
的分布列和期望;
(3)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业购买某种仪器,在仪器使用期间可能出现故障,需要请销售仪器的企业派工程师进行维修,因为考虑到人力、成本等多方面的原因,销售仪器的企业提供以下购买仪器维修服务的条件:在购买仪器时,可以直接购买仪器维修服务,维修一次1000元;在仪器使用期间,如果维修服务次数不够再次购买,则需要每次1500元..现需决策在购买仪器的同时购买几次仪器维修服务,为此搜集并整理了500台这种机器在使用期内需要维修的次数,得到如下表格:
维修次数 | 5 | 6 | 7 | 8 | 9 |
频数(台) | 50 | 100 | 150 | 100 | 100 |
记![]() 表示一台仪器使用期内维修的次数,
表示一台仪器使用期内维修的次数,![]() 表示一台仪器使用期内维修所需要的费用,
表示一台仪器使用期内维修所需要的费用,![]() 表示购买仪器的同时购买的维修服务的次数.
表示购买仪器的同时购买的维修服务的次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)以这500台仪器使用期内维修次数的频率代替一台仪器维修次数发生的概率,求![]() 的概率.
的概率.
(3)假设购买这500台仪器的同时每台都购买7次维修服务,或每台都购买8次维修服务,请分别计算这500台仪器在购买维修服务所需要费用的平均数,以此为决策依据,判断购买7次还是8次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人沿同一方向去C地,途中都使用两种不同的速度![]() .甲一半路程使用速度
.甲一半路程使用速度![]() ,另一半路程使用速度
,另一半路程使用速度![]() ,乙一半时间使用速度
,乙一半时间使用速度![]() ,另一半时间使用速度
,另一半时间使用速度![]() ,甲、乙两人从A地到C地的路程与时间的函数图象及关系,有下面图中4个不同的图示分析(其中横轴
,甲、乙两人从A地到C地的路程与时间的函数图象及关系,有下面图中4个不同的图示分析(其中横轴![]() 表示时间,纵轴
表示时间,纵轴![]() 表示路程),其中正确的图示分析为( ).
表示路程),其中正确的图示分析为( ).


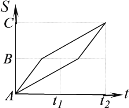

(1) (2) (3) (4)
A.(1)B.(3)C.(1)或(4)D.(1)或(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com