练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】甲、乙两人沿同一方向去C地，途中都使用两种不同的速度．甲一半路程使用速度，另一半路程使用速度，乙一半时间使用速度，另一半时间使用速度，甲、乙两人从A地到C地的路程与时间的函数图象及关系，有下面图中4个不同的图示分析（其中横轴表示时间，纵轴表示路程），其中正确的图示分析为（ ）．

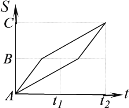
    （1） （2） （3） （4）

    A.(1)B.(3)C.(1)或(4)D.(1)或(2)

    【答案】C

    【解析】

    甲一半路程使用速度v1，另一半路程使用速度v2，因为v1＜v2，所以用速度v1走一半路程所用时间大于总时间的一半，同时，乙一半时间使用速度v1，另一半时间使用速度v2，在t1时间里所走的路程小于总路程是一半．

    根据题意，设A到C地路程为2S，到B地路程为S,

    则，从A到C地，甲用的时间为

    乙用的时间为

    分析可得t1＞t2，即乙比甲先到B地，进而可排除图（2）、（3）；

    当甲前一半路程速度为V1，后一半路程为V2时，因为v1＜v2，所以走前一半路程所用时间大于 ，图（4）正确，

    当甲前一半路程速度为V2，后一半路程为V1时，因为v1＜v2，所以走一半路程所用时间小于，图（1）正确，

    再验证乙的情况，可知图（1）、（4）也符合；故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，。

    （Ⅰ）若 ，求的值；

    （Ⅱ）讨论函数的单调性。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a、b、c为的三边长，直线l的方程，圆.

    （1）若为直角三角形，c为斜边长，且直线l与圆M相切，求c的值；

    （2）若为正三角形，对于直线l上任意一点P，在圆M上总存在一点Q，使得线段的长度为整数，求c的取值范围；

    （3）点，，，，设E、F、G、H四点到直线l的距离之和为S，求S的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来.随着计划生育政策效果的逐步显现以及老龄化的加剧，我国经济发展的“人口红利”在逐渐消退，在当前形势下，很多二线城市开始了“抢人大战”，自2018年起，像西安、南京等二线城市人才引进与落户等政策放宽力度空前，至2019年发布各种人才引进与落户等政策的城市已经有16个。某二线城市与2018年初制定人才引进与落户新政（即放宽政策，以下简称新政）：硕士研究生及以上可直接落户并享有当地政府依法给与的住房补贴，本科学历毕业生可以直接落户，专科学历毕业生在当地工作两年以上可以落户。高中及以下学历人员在当地工作10年以上可以落户。新政执行一年，2018年全年新增落户人口较2017年全年增加了一倍，为了深入了解新增落户人口结构及变化情况，相关部门统计了该市新政执行前一年（即2017年）与新政执行一年（即2018年）新增落户人口学历构成比例，得到如下饼图：

    则下面结论中错误的是（ ）

    A. 新政实施后，新增落户人员中本科生已经超过半数

    B. 新政实施后，高中及以下学历人员新增落户人口减少

    C. 新政对硕士研究生及以上的新增落户人口数量暂时未产生影响

    D. 新政对专科生在该市落实起到了积极的影响

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某机构为了了解不同年龄的人对一款智能家电的评价，随机选取了50名购买该家电的消费者，让他们根据实际使用体验进行评分.

    （Ⅰ）设消费者的年龄为，对该款智能家电的评分为.若根据统计数据，用最小二乘法得到关于的线性回归方程为，且年龄的方差为，评分的方差为.求与的相关系数，并据此判断对该款智能家电的评分与年龄的相关性强弱.

    （Ⅱ）按照一定的标准，将50名消费者的年龄划分为“青年”和“中老年”，评分划分为“好评”和“差评”，整理得到如下数据，请判断是否有的把握认为对该智能家电的评价与年龄有关.

    好评

    差评

    青年

    8

    16

    中老年

    20

    6

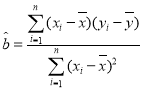    附：线性回归直线的斜率；相关系数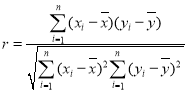，独立性检验中的，其中.

    临界值表：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年1月4日，据“央视财经”微信公众号消息，点外卖已成为众多消费者一大常规的就餐形式，外卖员也成为了一种职业.为调查某外卖平台外卖员的送餐收入，现从该平台随机抽取100名点外卖的用户进行统计，按送餐距离分类统计得如下频率分布直方图：

    将上述调查所得到的频率视为概率.

    （1）求的值，并估计利用该外卖平台点外卖用户的平均送餐距离；

    （2）若该外卖平台给外卖员的送餐费用与送餐距离有关，规定2千米内为短距离，每份3元，2千米到4千米为中距离，每份5元，超过4千米为远距离，每份9元.

    （i）记为外卖员送一份外卖的牧入（单位：元），求的分布列和数学期望；

    （ii）若外卖员一天的收入不低于150元，试利用上述数据估计该外卖员一天的送餐距离至少为多少千米？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．

    （1）若曲线在处切线的斜率为，求此切线方程；

    （2）若有两个极值点，求的取值范围，并证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四边形ABED中，AB//DE，ABBE，点C在AB上，且ABCD，AC=BC=CD=2，现将△ACD沿CD折起，使点A到达点P的位置，且PE.

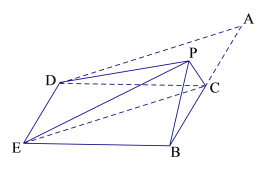
    （1）求证：平面PBC 平面DEBC；

    （2）求三棱锥P-EBC的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一所学校计划举办“国学”系列讲座.由于条件限制，按男、女生比例采用分层抽样的方法，从某班选出10人参加活动.在活动前对所选的10名同学进行了国学素养测试，这10名同学的性别和测试成绩（百分制）的茎叶图如图.

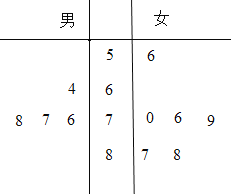
    （1）根据这10名同学的测试成绩，估计该班男、女生国学素养测试的平均成绩；

    （2）若成绩大于等于75分为优良，从这10名同学中随机选取2名男生，2名女生，求这4名同学的国学素养测试成绩均为优良的概率.

    查看答案和解析>>

    同步练习册答案