
【题目】已知椭圆![]() 的长轴长为4,且经过点
的长轴长为4,且经过点 .
.
(1)求椭圆的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,且与椭圆相交于
,且与椭圆相交于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),过
),过![]() 作
作![]() 的角平分线交椭圆于另一点
的角平分线交椭圆于另一点![]() .证明:直线
.证明:直线![]() 与坐标轴平行.
与坐标轴平行.
科目:高中数学 来源: 题型:
【题目】设经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,经过点
两点,经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() .
.
(1)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(2)问是否存在直线![]() ,
,![]() 使得
使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国改革开放以来经济发展迅猛,某一线城市的城镇居民2012~2018年人均可支配月收入散点图如下(年份均用末位数字减1表示).
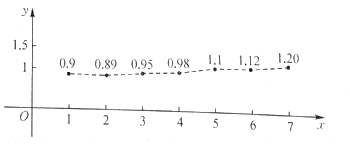
(1)由散点图可知,人均可支配月收入y(万元)与年份x之间具有较强的线性相关关系,试求y关于x的回归方程(系数精确到0.001),依此相关关系预测2019年该城市人均可支配月收入;
(2)在2014~2018年的五个年份中随机抽取两个数据作样本分析,求所取的两个数据中,人均可支配月收入恰好有一个超过1万元的概率.
注: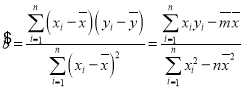 ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】概率论起源于博弈游戏.17世纪,曾有一个“赌金分配“的问题:博弈水平相当的甲、乙两人进行博弈游戏,每局比赛都能分出胜负,没有平局.双方约定,各出赌金48枚金币,先赢3局者可获得全部赌金;但比赛中途因故终止了,此时甲赢了2局,乙赢了1局.向这96枚金币的赌金该如何分配?数学家费马和帕斯卡都用了现在称之为“概率“的知识,合理地给出了赌金分配方案.该分配方案是( )
A.甲48枚,乙48枚B.甲64枚,乙32枚
C.甲72枚,乙24枚D.甲80枚,乙16枚
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到,任画一条线段,然后把它均分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”;用同样的方法把每条小线段重复上述步骤,得到16条更小的线段构成的折线,称为“二次构造”,…,如此进行“![]() 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取
次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取![]() ,
,![]() )
)
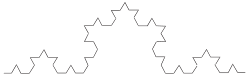
A.16B.17C.24D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.
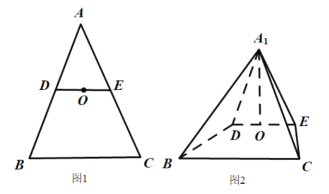
(1)求证:![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com